Advertisements
Advertisements
प्रश्न
Find the area of the region bounded by \[y = \sqrt{x}\] and y = x.
उत्तर
The curve\[y = \sqrt{x}\] or \[y^2 = x\] represents a parabola opening towards the positive x-axis.
The curve y = x represents a line passing through the origin.
Solving \[y^2 = x\] and y = x, we get \[x^2 = x\]
\[ \Rightarrow x^2 - x = 0\]
\[ \Rightarrow x\left( x - 1 \right) = 0\]
\[ \Rightarrow x = 0\text{ or }x = 1\]
Thus, the given curves intersect at O(0, 0) and A(1, 1).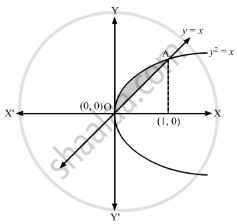
∴ Required area = Area of the shaded region OAO
\[= \int_0^1 y_{\text{ parabola }} dx - \int_0^1 y_{\text{ line }} dx\]
\[ = \int_0^1 \sqrt{x}dx - \int_0^1 xdx\]
\[ = \left.\frac{x^\frac{3}{2}}{\frac{3}{2}}\right|_0^1 - \left.\frac{x^2}{2}\right|_0^1 \]
\[ = \frac{2}{3}\left( 1 - 0 \right) - \frac{1}{2}\left( 1 - 0 \right)\]
\[ = \frac{2}{3} - \frac{1}{2}\]
\[ = \frac{1}{6}\text{ square units }\]
APPEARS IN
संबंधित प्रश्न
Using the method of integration, find the area of the triangular region whose vertices are (2, -2), (4, 3) and (1, 2).
Draw a rough sketch of the graph of the function y = 2 \[\sqrt{1 - x^2}\] , x ∈ [0, 1] and evaluate the area enclosed between the curve and the x-axis.
Using definite integrals, find the area of the circle x2 + y2 = a2.
Using integration, find the area of the region bounded by the following curves, after making a rough sketch: y = 1 + | x + 1 |, x = −2, x = 3, y = 0.
Draw a rough sketch of the curve \[y = \frac{x}{\pi} + 2 \sin^2 x\] and find the area between the x-axis, the curve and the ordinates x = 0 and x = π.
Find the area bounded by the curve y = 4 − x2 and the lines y = 0, y = 3.
Find the area of the region \[\left\{ \left( x, y \right): \frac{x^2}{a^2} + \frac{y^2}{b^2} \leq 1 \leq \frac{x}{a} + \frac{y}{b} \right\}\]
Using integration, find the area of the region bounded by the triangle whose vertices are (2, 1), (3, 4) and (5, 2).
Find the area of the region bounded by \[y = \sqrt{x}, x = 2y + 3\] in the first quadrant and x-axis.
Find the area, lying above x-axis and included between the circle x2 + y2 = 8x and the parabola y2 = 4x.
Prove that the area common to the two parabolas y = 2x2 and y = x2 + 4 is \[\frac{32}{3}\] sq. units.
Find the area of the region bounded by the parabola y2 = 2x + 1 and the line x − y − 1 = 0.
Sketch the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 1. Also, find the area of this region.
Using integration find the area of the region:
\[\left\{ \left( x, y \right) : \left| x - 1 \right| \leq y \leq \sqrt{5 - x^2} \right\}\]
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2= 32.
Find the area enclosed by the curves y = | x − 1 | and y = −| x − 1 | + 1.
Find the area of the region between the parabola x = 4y − y2 and the line x = 2y − 3.
The area bounded by the curves y = sin x between the ordinates x = 0, x = π and the x-axis is _____________ .
The area bounded by the curve y = f (x), x-axis, and the ordinates x = 1 and x = b is (b −1) sin (3b + 4). Then, f (x) is __________ .
Area bounded by the curve y = x3, the x-axis and the ordinates x = −2 and x = 1 is ______.
The area bounded by the curve y = x |x| and the ordinates x = −1 and x = 1 is given by
The area of the circle x2 + y2 = 16 enterior to the parabola y2 = 6x is
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
Using integration, find the area of the region bounded by the line x – y + 2 = 0, the curve x = \[\sqrt{y}\] and y-axis.
Sketch the graphs of the curves y2 = x and y2 = 4 – 3x and find the area enclosed between them.
Find the area of the region bound by the curves y = 6x – x2 and y = x2 – 2x
The area of the region bounded by the curve y = x2 + x, x-axis and the line x = 2 and x = 5 is equal to ______.
Find the area bounded by the curve y = sinx between x = 0 and x = 2π.
The area of the region bounded by the curve y = `sqrt(16 - x^2)` and x-axis is ______.
Using integration, find the area of the region `{(x, y): 0 ≤ y ≤ sqrt(3)x, x^2 + y^2 ≤ 4}`
The curve x = t2 + t + 1,y = t2 – t + 1 represents
Area lying in the first quadrant and bounded by the circle `x^2 + y^2 = 4` and the lines `x + 0` and `x = 2`.
Find the area of the region bounded by `x^2 = 4y, y = 2, y = 4`, and the `y`-axis in the first quadrant.
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9` = 1.
Find the area of the region enclosed by the curves y2 = x, x = `1/4`, y = 0 and x = 1, using integration.
The area enclosed by y2 = 8x and y = `sqrt(2x)` that lies outside the triangle formed by y = `sqrt(2x)`, x = 1, y = `2sqrt(2)`, is equal to ______.
The area (in sq.units) of the region A = {(x, y) ∈ R × R/0 ≤ x ≤ 3, 0 ≤ y ≤ 4, y ≤x2 + 3x} is ______.
Make a rough sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 1, 0 ≤ y ≤ x + 1, 0 ≤ x ≤ 2} and find the area of the region, using the method of integration.
Hence find the area bounded by the curve, y = x |x| and the coordinates x = −1 and x = 1.
