Question

Find the area enclosed by the curves y = | x − 1 | and y = −| x − 1 | + 1.

Answer 1

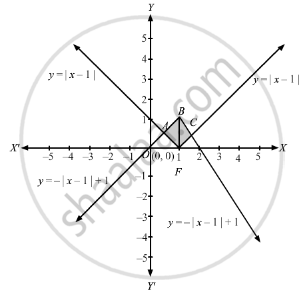
The given curves are \[y = \left| x - 1 \right| . . . . . \left( 1 \right)\]
\[y = - \left| x - 1 \right| + 1 . . . . . \left( 2 \right)\]
Clearly \[y = \left| x - 1 \right|\]  is cutting the x-axis  at (1, 0) and the y-axis at (0, 1) respectively.
Also \[y = - \left| x - 1 \right| + 1\]  is cutting both the axes at (0, 0) and x-axis at (2, 0).
We have,
\[y = \left| x - 1 \right|\]
\[y = \begin{cases}x - 1& x \geq 1\\1 - x& x < 1\end{cases}\]
And
\[y = - \left| x - 1 \right| + 1\]
\[y = \begin{cases}2 - x &x \geq 1\\ x &x < 1\end{cases}\]
\[\text{ Solving both the equations for }x < 1\]
\[y = 1 - x\text{ and }y = x, \]
\[\text{ We get }x = \frac{1}{2}\text{ and }y = \frac{1}{2}\]
\[\text{ And solving both the equations for }x \geq 1\]
\[y = x - 1\text{ and }y = 2 - x, \]
\[\text{ We get }x = \frac{3}{2}\text{ and }y = \frac{1}{2}\]
Thus  the intersecting points are \[\left( \frac{1}{2}, \frac{1}{2} \right)\] and \[\left( \frac{3}{2}, \frac{1}{2} \right)\] 
The required area A = ( Area of  ABFA  + Area of  BCFB)
Now approximating the area of ABFA  the length = \[\left| y_1 \right|\]  and width  = dx

Area of  ABFA

\[= \int_\frac{1}{2}^1 \left[ x - \left( 1 - x \right) \right] d x\]
\[ = \int_\frac{1}{2}^1 \left( 2x - 1 \right) d x\]
\[ = \left[ x^2 - x \right]_\frac{1}{2}^1 \]
\[ = \frac{1}{4}\]
Similarly approximating the area of  BCFB the length \[= \left| y_2 \right|\]  and  width= dx

Area of  BCFB 
\[= \int_1^\frac{3}{2} \left[ \left( 2 - x \right) - \left( x - 1 \right) \right] d x\]
\[ = \int_1^\frac{3}{2} \left( 3 - 2x \right) d x\]
\[ = \left[ 3x - x^2 \right]_1^\frac{3}{2} \]
\[ = \frac{1}{4}\]
Thus the required area A =( Area of ABFA  + Area of BCFB)

\[= \frac{1}{4} + \frac{1}{4} = \frac{1}{2}\]
Hence the required area is \[\frac{1}{2}\]  square units.