Advertisements
Advertisements
प्रश्न
Find the area bounded by the parabola x = 8 + 2y − y2; the y-axis and the lines y = −1 and y = 3.
Advertisements
उत्तर
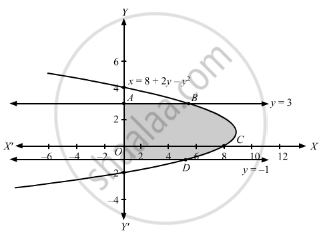
The parabola cuts y-axis at (0, 4) and (0, −2).
Also, the points of intersection of the parabola and the lines y = 3 and y = −1 are B(5, 3) and D(5, −1) respectively.
Therefore, the area of the required region ABCDE
\[A = \int_{- 1}^3 x d y\]
\[ = \int_{- 1}^3 \left( 8 + 2y - y^2 \right) d y\]
\[ = \left[ 8y + y^2 - \frac{y^3}{3} \right]_{- 1}^3 \]
\[ = \left\{ 8\left( 3 \right) + \left( 3 \right)^2 - \frac{\left( 3 \right)^3}{3} \right\} - \left\{ 8\left( - 1 \right) + \left( - 1 \right)^2 - \frac{\left( - 1 \right)^3}{3} \right\}\]
\[ = \left\{ 24 + 9 - 9 \right\} - \left\{ - 8 + 1 + \frac{1}{3} \right\}\]
\[ = \left( 24 \right) - \left\{ - 7 + \frac{1}{3} \right\}\]
\[ = 24 + 7 - \frac{1}{3}\]
\[ = 31 - \frac{1}{3}\]
\[ = \frac{92}{3}\text{ sq . units }\]
APPEARS IN
संबंधित प्रश्न
Find the area of the region bounded by the parabola y2 = 4ax and its latus rectum.
Find the area of the region bounded by the parabola y2 = 16x and the line x = 3.
Area bounded by the curve y = x3, the x-axis and the ordinates x = –2 and x = 1 is ______.
Sketch the graph of y = \[\sqrt{x + 1}\] in [0, 4] and determine the area of the region enclosed by the curve, the x-axis and the lines x = 0, x = 4.
Find the area under the curve y = \[\sqrt{6x + 4}\] above x-axis from x = 0 to x = 2. Draw a sketch of curve also.
Using integration, find the area of the region bounded by the following curves, after making a rough sketch: y = 1 + | x + 1 |, x = −2, x = 3, y = 0.
Find the area of the region bounded by the curve xy − 3x − 2y − 10 = 0, x-axis and the lines x = 3, x = 4.
Draw a rough sketch of the curve \[y = \frac{x}{\pi} + 2 \sin^2 x\] and find the area between the x-axis, the curve and the ordinates x = 0 and x = π.
Find the area of the minor segment of the circle \[x^2 + y^2 = a^2\] cut off by the line \[x = \frac{a}{2}\]
Find the area of the region between the circles x2 + y2 = 4 and (x − 2)2 + y2 = 4.
Find the area bounded by the parabola y = 2 − x2 and the straight line y + x = 0.
Using integration find the area of the region:
\[\left\{ \left( x, y \right) : \left| x - 1 \right| \leq y \leq \sqrt{5 - x^2} \right\}\]
Find the area of the region {(x, y): x2 + y2 ≤ 4, x + y ≥ 2}.
Find the area enclosed by the curves 3x2 + 5y = 32 and y = | x − 2 |.
If the area bounded by the parabola \[y^2 = 4ax\] and the line y = mx is \[\frac{a^2}{12}\] sq. units, then using integration, find the value of m.
If the area enclosed by the parabolas y2 = 16ax and x2 = 16ay, a > 0 is \[\frac{1024}{3}\] square units, find the value of a.
The area included between the parabolas y2 = 4x and x2 = 4y is (in square units)
The area bounded by the parabola x = 4 − y2 and y-axis, in square units, is ____________ .
The area of the region bounded by the parabola y = x2 + 1 and the straight line x + y = 3 is given by
Area bounded by parabola y2 = x and straight line 2y = x is _________ .
The area of the circle x2 + y2 = 16 enterior to the parabola y2 = 6x is
Area lying in first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2, is
Find the coordinates of a point of the parabola y = x2 + 7x + 2 which is closest to the straight line y = 3x − 3.
Find the area of the region bound by the curves y = 6x – x2 and y = x2 – 2x
Using the method of integration, find the area of the region bounded by the lines 3x − 2y + 1 = 0, 2x + 3y − 21 = 0 and x − 5y + 9 = 0
Using integration, find the area of the smaller region bounded by the ellipse `"x"^2/9+"y"^2/4=1`and the line `"x"/3+"y"/2=1.`
Find the area bounded by the curve y = sinx between x = 0 and x = 2π.
The area of the region bounded by the circle x2 + y2 = 1 is ______.
Using integration, find the area of the region bounded between the line x = 4 and the parabola y2 = 16x.
The curve x = t2 + t + 1,y = t2 – t + 1 represents
Let f(x) be a continuous function such that the area bounded by the curve y = f(x), x-axis and the lines x = 0 and x = a is `a^2/2 + a/2 sin a + pi/2 cos a`, then `f(pi/2)` =
Find the area of the region bounded by the curve `y^2 - x` and the line `x` = 1, `x` = 4 and the `x`-axis.
What is the area of the region bounded by the curve `y^2 = 4x` and the line `x` = 3.
Find the area of the region bounded by the curve `y = x^2 + 2, y = x, x = 0` and `x = 3`
The area bounded by the curve `y = x|x|`, `x`-axis and the ordinate `x` = – 1 and `x` = 1 is given by
Find the area of the region enclosed by the curves y2 = x, x = `1/4`, y = 0 and x = 1, using integration.
The area enclosed by y2 = 8x and y = `sqrt(2x)` that lies outside the triangle formed by y = `sqrt(2x)`, x = 1, y = `2sqrt(2)`, is equal to ______.
Let T be the tangent to the ellipse E: x2 + 4y2 = 5 at the point P(1, 1). If the area of the region bounded by the tangent T, ellipse E, lines x = 1 and x = `sqrt(5)` is `sqrt(5)`α + β + γ `cos^-1(1/sqrt(5))`, then |α + β + γ| is equal to ______.
Using integration, find the area of the region bounded by line y = `sqrt(3)x`, the curve y = `sqrt(4 - x^2)` and Y-axis in first quadrant.
