Advertisements
Advertisements
प्रश्न
The area bounded by `y`-axis, `y = cosx` and `y = sinx, 0 ≤ x - (<pi)/2` is
पर्याय
`2(sqrt(2) - 1)`
`sqrt(2) - 1`
`sqrt(2) + 1`
`sqrt(2)`
उत्तर
`sqrt(2) - 1`
Explanation:
The curves are `y = cosx, y = sin x, 0 ≤ x - (<pi)/2`
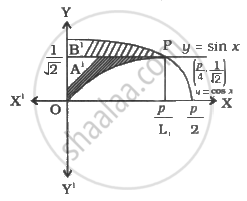
The curves meet where `sin x = cos x` to `tan x = 1`
⇒ `x = pi/2, sin pi/4 = cos pi/4 = 1/sqrt(2)`
Graphs of these curve is as shown in figure.
They intersect at `P(pi/4, 1/sqrt(2))`
The area bounded by `y`-axis, `y = cos x` and `y = sin x(0 ≤ x (<pi)/2)`
= Shaded area = Area of region ΔOPBO
= Area of region ΔPAO + Area of region ΔPBA
= `int_0^(1/sqrt(2)) sin^-1 ydy + int_(1/sqrt(2))^1 cos^-1 ydy`
= Integrating each by parts taking II as first function
A = `[y sin^-1 y - int 1/sqrt(1 - y^2) * ydy]_0^(1/sqrt(2)) + [y cos^-1 y + int 1/sqrt(1 - y^2) y dy]_(1/sqrt(2))^1`
= `[y sin^-1 y + sqrt(1 - y^2)]_0^(1/sqrt(2)) + [y cos^-1 y - sqrt(1 - y^2)]_(1/sqrt(2))^1`
= `[1/sqrt(2) sin^-1 1/sqrt(2) + sqrt(1/2) - 1] + [(cos^-1 - 0) - (1/sqrt(2) cos^-1 1/sqrt(2) - 1/sqrt(2))]`
= `(1/sqrt(2) * pi/4 + 1/sqrt(2)) + (0 - 1/sqrt(2) * pi/4 + 1/sqrt(2))`
= `2 xx 1/sqrt(2) - 1`
= `sqrt(2) - 1`.
