Advertisements
Advertisements
प्रश्न
The area of the region bounded by the curve x = 2y + 3 and the y lines. y = 1 and y = –1 is ______.
पर्याय
4 sq.units
`3/2` sq units
6 sq.units
8 sq.units
उत्तर
The area of the region bounded by the curve x = 2y + 3 and the y lines. y = 1 and y = –1 is 6 sq.units.
Explanation:
Given equations of lines are x = 2y + 3, y = 1 and y = –1
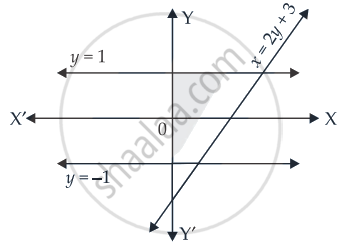
Required area = `int_-1^1 (2y + 3) "d"y`
= `2 * 1/2 [y^2]_-1^1 + 3[y]_-1^1`
= `(1 - 1) + 3(1 + 1)`
= 6 sq.units
APPEARS IN
संबंधित प्रश्न
Using integration, find the area bounded by the curve x2 = 4y and the line x = 4y − 2.
Find the area of the region bounded by the parabola y2 = 16x and the line x = 3.
Find the area of the region common to the circle x2 + y2 =9 and the parabola y2 =8x
Sketch the region bounded by the curves `y=sqrt(5-x^2)` and y=|x-1| and find its area using integration.
Area bounded by the curve y = x3, the x-axis and the ordinates x = –2 and x = 1 is ______.
The area bounded by the curve y = x | x|, x-axis and the ordinates x = –1 and x = 1 is given by ______.
[Hint: y = x2 if x > 0 and y = –x2 if x < 0]
Sketch the graph y = | x − 5 |. Evaluate \[\int\limits_0^1 \left| x - 5 \right| dx\]. What does this value of the integral represent on the graph.
Find the area of the region bounded by the curve xy − 3x − 2y − 10 = 0, x-axis and the lines x = 3, x = 4.
Find the area of the region bounded by the curve \[x = a t^2 , y = 2\text{ at }\]between the ordinates corresponding t = 1 and t = 2.
Prove that the area in the first quadrant enclosed by the x-axis, the line x = \[\sqrt{3}y\] and the circle x2 + y2 = 4 is π/3.
Find the area, lying above x-axis and included between the circle x2 + y2 = 8x and the parabola y2 = 4x.
Using integration, find the area of the following region: \[\left\{ \left( x, y \right) : \frac{x^2}{9} + \frac{y^2}{4} \leq 1 \leq \frac{x}{3} + \frac{y}{2} \right\}\]
Find the area enclosed by the curves 3x2 + 5y = 32 and y = | x − 2 |.
In what ratio does the x-axis divide the area of the region bounded by the parabolas y = 4x − x2 and y = x2− x?
The area bounded by the parabola x = 4 − y2 and y-axis, in square units, is ____________ .
The area of the region bounded by the parabola y = x2 + 1 and the straight line x + y = 3 is given by
Area of the region bounded by the curve y2 = 4x, y-axis and the line y = 3, is
Find the area of the region bounded by the curve ay2 = x3, the y-axis and the lines y = a and y = 2a.
The area of the region bounded by the curve y = x2 and the line y = 16 ______.
Find the area of the region bounded by the curve y2 = 4x, x2 = 4y.
Compute the area bounded by the lines x + 2y = 2, y – x = 1 and 2x + y = 7.
Find the area bounded by the lines y = 4x + 5, y = 5 – x and 4y = x + 5.
Find the area of the region bounded by the curve `y^2 - x` and the line `x` = 1, `x` = 4 and the `x`-axis.
Find the area of the region bounded by curve 4x2 = y and the line y = 8x + 12, using integration.
Using integration, find the area of the region bounded by the curves x2 + y2 = 4, x = `sqrt(3)`y and x-axis lying in the first quadrant.
Find the area of the region enclosed by the curves y2 = x, x = `1/4`, y = 0 and x = 1, using integration.
Let T be the tangent to the ellipse E: x2 + 4y2 = 5 at the point P(1, 1). If the area of the region bounded by the tangent T, ellipse E, lines x = 1 and x = `sqrt(5)` is `sqrt(5)`α + β + γ `cos^-1(1/sqrt(5))`, then |α + β + γ| is equal to ______.
The area of the region S = {(x, y): 3x2 ≤ 4y ≤ 6x + 24} is ______.
Find the area of the region bounded by the curve x2 = 4y and the line x = 4y – 2.
