Advertisements
Advertisements
प्रश्न
Find the area of the region bounded by the curve x2 = 4y and the line x = 4y – 2.
उत्तर
Curve x2 = 4y ...(1)
Line x = 4y – 2 ...(2)
Solving (1) and (2)
x = x2 – 2
`\implies` x2 – x – 2 = 0
(x – 2)(x + 1) = 0
∴ x = 2, – 1
∴ y = `x^2/4 = 1, 1/4`
Points of intersection are `A(2, 1), B(-1, 1/4)`
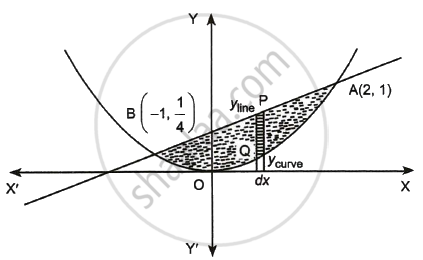
The shaded region is required.
Let PQ to be the elementary strip.
So area of shaded region
= `int_-1^2 (y_"line" - y_"curve")dx`
= `int_-1^2 (x + 2)/4 - x^2/4dx`
= `1/4[x^2/2 + 2x - x^3/3]_-1^2`
= `1/4[(4/2 + 4 - 8/3)] - [(1/2 - 2 + 1/3)]`
= `1/4[6 - 8/3 - 1/2 + 2 - 1/3]`
= `1/4[6 - 9/3 - 1/2 + 2]`
= `1/4[6 - 3 - 1/2 + 2]`
= `1/4 xx 9/2`
= `9/8` sq.units
APPEARS IN
संबंधित प्रश्न
Using integration, find the area of the region bounded by the lines y = 2 + x, y = 2 – x and x = 2.
Find the area of the region bounded by the parabola y2 = 4ax and the line x = a.
Find the area under the curve y = \[\sqrt{6x + 4}\] above x-axis from x = 0 to x = 2. Draw a sketch of curve also.
Using definite integrals, find the area of the circle x2 + y2 = a2.
Find the area of the region in the first quadrant bounded by the parabola y = 4x2 and the lines x = 0, y = 1 and y = 4.
Find the area of the region bounded by x2 = 4ay and its latusrectum.
Find the area of the region common to the parabolas 4y2 = 9x and 3x2 = 16y.
Using integration, find the area of the region bounded by the triangle ABC whose vertices A, B, C are (−1, 1), (0, 5) and (3, 2) respectively.
Draw a rough sketch and find the area of the region bounded by the two parabolas y2 = 4x and x2 = 4y by using methods of integration.
Find the area bounded by the curves x = y2 and x = 3 − 2y2.
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2= 32.
Using integration find the area of the region bounded by the curves \[y = \sqrt{4 - x^2}, x^2 + y^2 - 4x = 0\] and the x-axis.
The area bounded by y = 2 − x2 and x + y = 0 is _________ .
The area bounded by the parabola x = 4 − y2 and y-axis, in square units, is ____________ .
The area of the region bounded by the parabola (y − 2)2 = x − 1, the tangent to it at the point with the ordinate 3 and the x-axis is _________ .
The area bounded by the curve y = x4 − 2x3 + x2 + 3 with x-axis and ordinates corresponding to the minima of y is _________ .
Using integration, find the area of the smaller region bounded by the ellipse `"x"^2/9+"y"^2/4=1`and the line `"x"/3+"y"/2=1.`
Find the area of the region bounded by the parabola y2 = 2x and the straight line x – y = 4.
The area of the region bounded by the curve x = y2, y-axis and the line y = 3 and y = 4 is ______.
Find the area bounded by the curve y = `sqrt(x)`, x = 2y + 3 in the first quadrant and x-axis.
Draw a rough sketch of the region {(x, y) : y2 ≤ 6ax and x 2 + y2 ≤ 16a2}. Also find the area of the region sketched using method of integration.
The area of the region bounded by the ellipse `x^2/25 + y^2/16` = 1 is ______.
The area of the region bounded by the circle x2 + y2 = 1 is ______.
Using integration, find the area of the region bounded between the line x = 4 and the parabola y2 = 16x.
Using integration, find the area of the region in the first quadrant enclosed by the line x + y = 2, the parabola y2 = x and the x-axis.
Find the area of the region bounded by curve 4x2 = y and the line y = 8x + 12, using integration.
For real number a, b (a > b > 0),
let Area `{(x, y): x^2 + y^2 ≤ a^2 and x^2/a^2 + y^2/b^2 ≥ 1}` = 30π
Area `{(x, y): x^2 + y^2 ≥ b^2 and x^2/a^2 + y^2/b^2 ≤ 1}` = 18π.
Then the value of (a – b)2 is equal to ______.
Let the curve y = y(x) be the solution of the differential equation, `("dy")/("d"x) = 2(x + 1)`. If the numerical value of area bounded by the curve y = y(x) and x-axis is `(4sqrt(8))/3`, then the value of y(1) is equal to ______.
Find the area of the minor segment of the circle x2 + y2 = 4 cut off by the line x = 1, using integration.
Make a rough sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 1, 0 ≤ y ≤ x + 1, 0 ≤ x ≤ 2} and find the area of the region, using the method of integration.
