Advertisements
Advertisements
Question
Find the area of the region bounded by the curve x2 = 4y and the line x = 4y – 2.
Solution
Curve x2 = 4y ...(1)
Line x = 4y – 2 ...(2)
Solving (1) and (2)
x = x2 – 2
`\implies` x2 – x – 2 = 0
(x – 2)(x + 1) = 0
∴ x = 2, – 1
∴ y = `x^2/4 = 1, 1/4`
Points of intersection are `A(2, 1), B(-1, 1/4)`
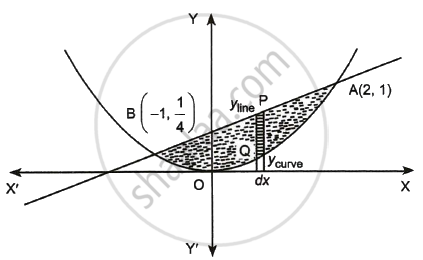
The shaded region is required.
Let PQ to be the elementary strip.
So area of shaded region
= `int_-1^2 (y_"line" - y_"curve")dx`
= `int_-1^2 (x + 2)/4 - x^2/4dx`
= `1/4[x^2/2 + 2x - x^3/3]_-1^2`
= `1/4[(4/2 + 4 - 8/3)] - [(1/2 - 2 + 1/3)]`
= `1/4[6 - 8/3 - 1/2 + 2 - 1/3]`
= `1/4[6 - 9/3 - 1/2 + 2]`
= `1/4[6 - 3 - 1/2 + 2]`
= `1/4 xx 9/2`
= `9/8` sq.units
APPEARS IN
RELATED QUESTIONS
Find the area of the region bounded by the parabola y2 = 4ax and its latus rectum.
Using integration, find the area bounded by the curve x2 = 4y and the line x = 4y − 2.
Find the area of ellipse `x^2/1 + y^2/4 = 1`
Draw a rough sketch of the curve and find the area of the region bounded by curve y2 = 8x and the line x =2.
Draw a rough sketch of the graph of the curve \[\frac{x^2}{4} + \frac{y^2}{9} = 1\] and evaluate the area of the region under the curve and above the x-axis.
Sketch the graph y = | x + 3 |. Evaluate \[\int\limits_{- 6}^0 \left| x + 3 \right| dx\]. What does this integral represent on the graph?
Find the area enclosed by the curve x = 3cost, y = 2sin t.
Find the area of the region bounded by x2 = 16y, y = 1, y = 4 and the y-axis in the first quadrant.
Find the area of the region included between the parabola y2 = x and the line x + y = 2.
Find the area of the region bounded by \[y = \sqrt{x}, x = 2y + 3\] in the first quadrant and x-axis.
Prove that the area common to the two parabolas y = 2x2 and y = x2 + 4 is \[\frac{32}{3}\] sq. units.
Find the area of the region bounded by the curves y = x − 1 and (y − 1)2 = 4 (x + 1).
Find the area of the region bounded by the curve y = \[\sqrt{1 - x^2}\], line y = x and the positive x-axis.
If the area enclosed by the parabolas y2 = 16ax and x2 = 16ay, a > 0 is \[\frac{1024}{3}\] square units, find the value of a.
If the area above the x-axis, bounded by the curves y = 2kx and x = 0, and x = 2 is \[\frac{3}{\log_e 2}\], then the value of k is __________ .
The closed area made by the parabola y = 2x2 and y = x2 + 4 is __________ .
The area bounded by the curve y2 = 8x and x2 = 8y is ___________ .
Find the coordinates of a point of the parabola y = x2 + 7x + 2 which is closest to the straight line y = 3x − 3.
Using integration, find the area of the region bounded by the line x – y + 2 = 0, the curve x = \[\sqrt{y}\] and y-axis.
The area of the region bounded by the curve y = x2 and the line y = 16 ______.
The area of the region bounded by the ellipse `x^2/25 + y^2/16` = 1 is ______.
The area of the region bounded by the circle x2 + y2 = 1 is ______.
Area of the region bounded by the curve y = |x + 1| + 1, x = –3, x = 3 and y = 0 is
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9` = 1.
The area of the region S = {(x, y): 3x2 ≤ 4y ≤ 6x + 24} is ______.
Area (in sq.units) of the region outside `|x|/2 + |y|/3` = 1 and inside the ellipse `x^2/4 + y^2/9` = 1 is ______.
Area of figure bounded by straight lines x = 0, x = 2 and the curves y = 2x, y = 2x – x2 is ______.
The area (in square units) of the region bounded by the curves y + 2x2 = 0 and y + 3x2 = 1, is equal to ______.
Using integration, find the area bounded by the curve y2 = 4ax and the line x = a.
Evaluate:
`int_0^1x^2dx`
