Advertisements
Advertisements
Question
Using integration, find the area bounded by the curve x2 = 4y and the line x = 4y − 2.
Solution
The area bounded by the curve, x2 = 4y, and line, x = 4y − 2, is represented by the shaded area OBAO.
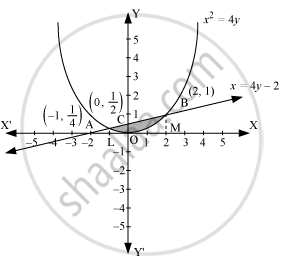
Let A and B be the points of intersection of the line and parabola.
Coordinates of point A are (-1, 1/4).
Coordinates of point B are (2, 1).
We draw AL and BM perpendicular to x-axis.
It can be observed that,
Area OBAO = Area OBCO + Area OACO … (1)
Then, Area OBCO = Area OMBC − Area OMBO
`=int_0^2(x+2)/4dx-int_0^2x^2/4dx`
`=1/4[x^2/2+2x]_0^2-1/4[x^3/3]_0^2`
`=-1/4[(-1)^2/2+2(-1)]-[1/4((-1)^3/3)]`
`=7/24`
Therefore, required area = `(5/6+7/24)=9/8 units`
APPEARS IN
RELATED QUESTIONS
Sketch the graph y = | x − 5 |. Evaluate \[\int\limits_0^1 \left| x - 5 \right| dx\]. What does this value of the integral represent on the graph.
Draw a rough sketch of the curve y = \[\frac{\pi}{2} + 2 \sin^2 x\] and find the area between x-axis, the curve and the ordinates x = 0, x = π.
Calculate the area of the region bounded by the parabolas y2 = x and x2 = y.
Using integration, find the area of the region bounded by the triangle ABC whose vertices A, B, C are (−1, 1), (0, 5) and (3, 2) respectively.
Find the area enclosed by the parabolas y = 5x2 and y = 2x2 + 9.
Prove that the area common to the two parabolas y = 2x2 and y = x2 + 4 is \[\frac{32}{3}\] sq. units.
Find the area of the region in the first quadrant enclosed by x-axis, the line y = \[\sqrt{3}x\] and the circle x2 + y2 = 16.
Find the area of the region bounded by the parabola y2 = 2x + 1 and the line x − y − 1 = 0.
Find the area enclosed by the curve \[y = - x^2\] and the straight line x + y + 2 = 0.
Find the area enclosed by the curves 3x2 + 5y = 32 and y = | x − 2 |.
The area of the region bounded by the parabola (y − 2)2 = x − 1, the tangent to it at the point with the ordinate 3 and the x-axis is _________ .
The area bounded by the parabola y2 = 4ax and x2 = 4ay is ___________ .
The closed area made by the parabola y = 2x2 and y = x2 + 4 is __________ .
Area of the region bounded by the curve y2 = 4x, y-axis and the line y = 3, is
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using vertical strips.
Find the area of the region bound by the curves y = 6x – x2 and y = x2 – 2x
Find the area of the region above the x-axis, included between the parabola y2 = ax and the circle x2 + y2 = 2ax.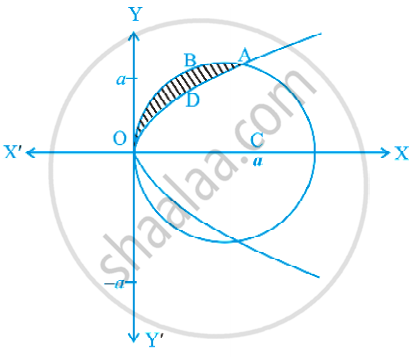
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2
Find the area bounded by the curve y = `sqrt(x)`, x = 2y + 3 in the first quadrant and x-axis.
Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32 is ______.
Area of the region bounded by the curve y = |x + 1| + 1, x = –3, x = 3 and y = 0 is
Make a rough sketch of the region {(x, y): 0 ≤ y ≤ x2, 0 ≤ y ≤ x, 0 ≤ x ≤ 2} and find the area of the region using integration.
Let f : [–2, 3] `rightarrow` [0, ∞) be a continuous function such that f(1 – x) = f(x) for all x ∈ [–2, 3]. If R1 is the numerical value of the area of the region bounded by y = f(x), x = –2, x = 3 and the axis of x and R2 = `int_-2^3 xf(x)dx`, then ______.
Let f(x) be a non-negative continuous function such that the area bounded by the curve y = f(x), x-axis and the ordinates x = `π/4` and x = `β > π/4` is `(βsinβ + π/4 cos β + sqrt(2)β)`. Then `f(π/2)` is ______.
Find the area of the minor segment of the circle x2 + y2 = 4 cut off by the line x = 1, using integration.
Using integration, find the area bounded by the curve y2 = 4ax and the line x = a.
