Advertisements
Advertisements
Question
Find the area of the minor segment of the circle x2 + y2 = 4 cut off by the line x = 1, using integration.
Solution
Given equation of circle x2 + y2 = 4
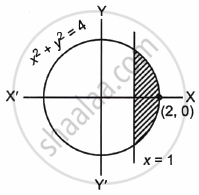
Required Area = `int_1^2 y dx`
= `2int_1^2 sqrt(4 - x^2)dx`
= `2[x/2 sqrt(4 - x^2) + 4/2 sin^-1 x/2]_1^2`
= `2[0 + 2 sin^-1 (1) - (1/2 sqrt(3) + 2 sin^-1 (1/2))]`
= `4(π/2) - sqrt(3) - 4(π/6)`
= `(2π - (2π)/3) - sqrt(3)`
= `(4π - 3sqrt(3))/3`
APPEARS IN
RELATED QUESTIONS
Find the area of the region bounded by the parabola y2 = 4ax and its latus rectum.
Find the area of the region bounded by the curve y = sinx, the lines x=-π/2 , x=π/2 and X-axis
triangle bounded by the lines y = 0, y = x and x = 4 is revolved about the X-axis. Find the volume of the solid of revolution.
Find the area of the sector of a circle bounded by the circle x2 + y2 = 16 and the line y = x in the ftrst quadrant.
Prove that the curves y2 = 4x and x2 = 4y divide the area of square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.
Using the method of integration find the area of the region bounded by lines: 2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0
Sketch the graph y = | x + 1 |. Evaluate\[\int\limits_{- 4}^2 \left| x + 1 \right| dx\]. What does the value of this integral represent on the graph?
Find the area of the region common to the parabolas 4y2 = 9x and 3x2 = 16y.
Find the area of the region bounded by \[y = \sqrt{x}, x = 2y + 3\] in the first quadrant and x-axis.
Find the area bounded by the lines y = 4x + 5, y = 5 − x and 4y = x + 5.
Find the area enclosed by the parabolas y = 4x − x2 and y = x2 − x.
In what ratio does the x-axis divide the area of the region bounded by the parabolas y = 4x − x2 and y = x2− x?
The area bounded by y = 2 − x2 and x + y = 0 is _________ .
The area of the region formed by x2 + y2 − 6x − 4y + 12 ≤ 0, y ≤ x and x ≤ 5/2 is ______ .
The area bounded by the y-axis, y = cos x and y = sin x when 0 ≤ x ≤ \[\frac{\pi}{2}\] is _________ .
Area lying in first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2, is
The area enclosed by the circle x2 + y2 = 2 is equal to ______.
Find the area of the region bounded by the curves y2 = 9x, y = 3x
Find the area of the region bounded by the curve y2 = 2x and x2 + y2 = 4x.
The area of the region bounded by parabola y2 = x and the straight line 2y = x is ______.
The area of the region bounded by the line y = 4 and the curve y = x2 is ______.
Smaller area bounded by the circle `x^2 + y^2 = 4` and the line `x + y = 2` is.
The area bounded by the curve `y = x^3`, the `x`-axis and ordinates `x` = – 2 and `x` = 1
The area bounded by `y`-axis, `y = cosx` and `y = sinx, 0 ≤ x - (<pi)/2` is
Make a rough sketch of the region {(x, y): 0 ≤ y ≤ x2, 0 ≤ y ≤ x, 0 ≤ x ≤ 2} and find the area of the region using integration.
Find the area of the region bounded by curve 4x2 = y and the line y = 8x + 12, using integration.
The area (in square units) of the region bounded by the curves y + 2x2 = 0 and y + 3x2 = 1, is equal to ______.
Find the area of the following region using integration ((x, y) : y2 ≤ 2x and y ≥ x – 4).
Evaluate:
`int_0^1x^2dx`
