Advertisements
Advertisements
Question
Find the area of the sector of a circle bounded by the circle x2 + y2 = 16 and the line y = x in the ftrst quadrant.
Solution

Given that x2 + y2 =16 ...(i)
y=x ...........(ii)
By equation (i) & (ii)
`x=+-2sqrt2`
`y=+-2sqrt2`
But required area in first quadrant
`x= y=2sqrt2`
`From dig. area = Area of Δ OBC + Area of region CABC`
`=int_o^(2sqrt2)x dx+int_(2sqrt2)^4sqrt(16-x^2)dx`
`=1/2 [x^2]_0^(2sqrt2)+[x/2sqrt(16-x^2)+16/2 sin^-1 (x/4)]_sqrt2^4`
`=4+8 xxpi/2-4-8xxpi/4=2pi sq.units`
APPEARS IN
RELATED QUESTIONS
Find the area of the region bounded by the parabola y2 = 4ax and its latus rectum.
Find the area of the region bounded by the curve y = sinx, the lines x=-π/2 , x=π/2 and X-axis
triangle bounded by the lines y = 0, y = x and x = 4 is revolved about the X-axis. Find the volume of the solid of revolution.
Area bounded by the curve y = x3, the x-axis and the ordinates x = –2 and x = 1 is ______.
Draw the rough sketch of y2 + 1 = x, x ≤ 2. Find the area enclosed by the curve and the line x = 2.
Draw a rough sketch of the graph of the curve \[\frac{x^2}{4} + \frac{y^2}{9} = 1\] and evaluate the area of the region under the curve and above the x-axis.
Draw a rough sketch of the curve y = \[\frac{\pi}{2} + 2 \sin^2 x\] and find the area between x-axis, the curve and the ordinates x = 0, x = π.
Find the area enclosed by the curve x = 3cost, y = 2sin t.
Find the area of the region in the first quadrant bounded by the parabola y = 4x2 and the lines x = 0, y = 1 and y = 4.
Find the area of the region bounded by x2 = 16y, y = 1, y = 4 and the y-axis in the first quadrant.
Draw a rough sketch of the region {(x, y) : y2 ≤ 5x, 5x2 + 5y2 ≤ 36} and find the area enclosed by the region using method of integration.
Draw a rough sketch and find the area of the region bounded by the two parabolas y2 = 4x and x2 = 4y by using methods of integration.
Using the method of integration, find the area of the region bounded by the following lines:
3x − y − 3 = 0, 2x + y − 12 = 0, x − 2y − 1 = 0.
Make a sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 3; 0 ≤ y ≤ 2x + 3; 0 ≤ x ≤ 3} and find its area using integration.
Find the area of the region enclosed between the two curves x2 + y2 = 9 and (x − 3)2 + y2 = 9.
Find the area enclosed by the curves y = | x − 1 | and y = −| x − 1 | + 1.
Find the area of the region bounded by the parabola y2 = 2x and the straight line x − y = 4.
The area included between the parabolas y2 = 4x and x2 = 4y is (in square units)
The area bounded by the curve y = loge x and x-axis and the straight line x = e is ___________ .
The area of the region bounded by the parabola (y − 2)2 = x − 1, the tangent to it at the point with the ordinate 3 and the x-axis is _________ .
The area bounded by the parabola y2 = 4ax and x2 = 4ay is ___________ .
The closed area made by the parabola y = 2x2 and y = x2 + 4 is __________ .
Area bounded by parabola y2 = x and straight line 2y = x is _________ .
Find the area of the region bounded by the parabolas y2 = 6x and x2 = 6y.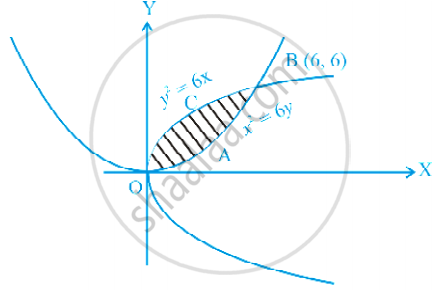
Find the area of the region above the x-axis, included between the parabola y2 = ax and the circle x2 + y2 = 2ax.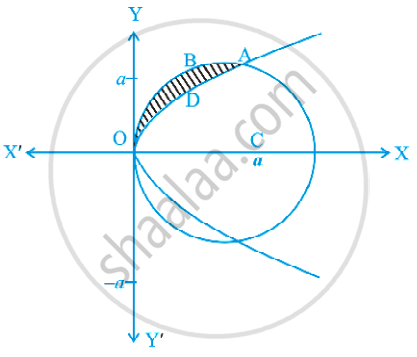
The area of the region bounded by the curve x = y2, y-axis and the line y = 3 and y = 4 is ______.
Area of the region bounded by the curve y = cosx between x = 0 and x = π is ______.
The area of the region bounded by the circle x2 + y2 = 1 is ______.
The area of the region bounded by the curve x = 2y + 3 and the y lines. y = 1 and y = –1 is ______.
Using integration, find the area of the region in the first quadrant enclosed by the line x + y = 2, the parabola y2 = x and the x-axis.
Find the area of the region bounded by `x^2 = 4y, y = 2, y = 4`, and the `y`-axis in the first quadrant.
Find the area of the region bounded by the curve `y = x^2 + 2, y = x, x = 0` and `x = 3`
Make a rough sketch of the region {(x, y): 0 ≤ y ≤ x2, 0 ≤ y ≤ x, 0 ≤ x ≤ 2} and find the area of the region using integration.
Find the area bounded by the curve y = |x – 1| and y = 1, using integration.
The area of the region S = {(x, y): 3x2 ≤ 4y ≤ 6x + 24} is ______.
Area of figure bounded by straight lines x = 0, x = 2 and the curves y = 2x, y = 2x – x2 is ______.
Let a and b respectively be the points of local maximum and local minimum of the function f(x) = 2x3 – 3x2 – 12x. If A is the total area of the region bounded by y = f(x), the x-axis and the lines x = a and x = b, then 4A is equal to ______.
Let g(x) = cosx2, f(x) = `sqrt(x)`, and α, β (α < β) be the roots of the quadratic equation 18x2 – 9πx + π2 = 0. Then the area (in sq. units) bounded by the curve y = (gof)(x) and the lines x = α, x = β and y = 0, is ______.
