Advertisements
Advertisements
Question
Using the method of integration, find the area of the region bounded by the following lines:
3x − y − 3 = 0, 2x + y − 12 = 0, x − 2y − 1 = 0.
Solution
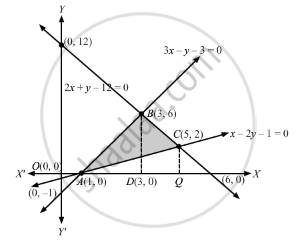
We have,
\[3x - y - 3 = 0 \cdots\left( 1 \right)\]
\[2x + y - 12 = 0 . . . \left( 2 \right)\]
\[x - 2y - 1 = 0 . . . \left( 3 \right)\]
\[\text{ Solving }\left( 1 \right)\text{ and }\left( 2 \right),\text{ we get, }\]
\[5x - 15 = 0 \]
\[ \Rightarrow x = 3 \]
\[ \therefore y = 6\]
\[B(3, 6)\text{ is point of intersection of }\left( 1 \right)\text{ and } \left( 2 \right)\]
\[\text{ Solving }\left( 1 \right)\text{ and }\left( 3 \right),\text{ we get, }\]
\[5x = 5\]
\[ \Rightarrow x = 1 \]
\[ \therefore y = 0\]
\[A\left( 1, 0 \right)\text{ is point of intersection of }\left( 1 \right)\text{ and }\left( 3 \right)\]
\[\text{ Solving }\left( 2 \right)\text{ and }\left( 3 \right),\text{ we get, }\]
\[5x = 25 \]
\[ \Rightarrow x = 5 \]
\[ \therefore y = 2\]
\[C\left( 5, 2 \right)\text{ is point of intersection of }\left( 2 \right)\text{ and }\left( 3 \right)\]
Now,
\[\text{ Area ABC }= \left\{\text{ area bound by }\left( 1 \right) \text{ between }x = 1\text{ and }x = 3 \right\} + \left\{\text{ area bound by }\left( 2 \right) between x = 3\text{ and }x = 5 \right\} - \left\{\text{ area bound by }\left( 3 \right) \text{ between }x = 1\text{ and }x = 5 \right\} \]
\[ = \int_1^3 \left( 3x - 3 \right) dx + \int_3^5 \left( 12 - 2x \right)dx - \int_1^5 \frac{\left( x - 1 \right)}{2}dx\]
\[ = \left[ 3 \times \frac{x^2}{2} - 3x \right]_1^3 + \left[ 12x - 2 \times \frac{x^2}{2} \right]_3^5 - \frac{1}{2} \left[ \frac{x^2}{2} - x \right]_1^5 \]
\[ = 3 \left[ \frac{x^2}{2} - x \right]_1^3 + \left[ 12x - x^2 \right]_3^5 - \frac{1}{2} \left[ \frac{x^2}{2} - x \right]_1^5 \]
\[ = 3\left( \frac{9}{2} - 3 \right) - 3\left( \frac{1}{2} - 1 \right) + \left( 12 - 25 \right) - \left( 12 - 9 \right) - \frac{1}{2}\left[ \left( \frac{25}{2} - 1 \right) - \left( \frac{1}{2} - 1 \right) \right]\]
\[ = 6 + 8 - 4\]
\[ = 10 \text{ sq units }\]
APPEARS IN
RELATED QUESTIONS
Sketch the region bounded by the curves `y=sqrt(5-x^2)` and y=|x-1| and find its area using integration.
Find the area of ellipse `x^2/1 + y^2/4 = 1`
Find the area of the region bounded by the parabola y2 = 4ax and the line x = a.
Find the area lying above the x-axis and under the parabola y = 4x − x2.
Determine the area under the curve y = \[\sqrt{a^2 - x^2}\] included between the lines x = 0 and x = a.
Using integration, find the area of the region bounded by the line 2y = 5x + 7, x-axis and the lines x = 2 and x = 8.
Draw a rough sketch of the curve y = \[\frac{\pi}{2} + 2 \sin^2 x\] and find the area between x-axis, the curve and the ordinates x = 0, x = π.
Using integration, find the area of the region bounded by the triangle whose vertices are (2, 1), (3, 4) and (5, 2).
Using integration, find the area of the region bounded by the triangle ABC whose vertices A, B, C are (−1, 1), (0, 5) and (3, 2) respectively.
Using integration, find the area of the triangular region, the equations of whose sides are y = 2x + 1, y = 3x+ 1 and x = 4.
Find the area of the region common to the circle x2 + y2 = 16 and the parabola y2 = 6x.
Prove that the area in the first quadrant enclosed by the x-axis, the line x = \[\sqrt{3}y\] and the circle x2 + y2 = 4 is π/3.
Find the area, lying above x-axis and included between the circle x2 + y2 = 8x and the parabola y2 = 4x.
Using integration, find the area of the region bounded by the triangle whose vertices are (−1, 2), (1, 5) and (3, 4).
Find the area enclosed by the curve \[y = - x^2\] and the straight line x + y + 2 = 0.
Find the area of the region bounded by the curve y = \[\sqrt{1 - x^2}\], line y = x and the positive x-axis.
Find the area bounded by the lines y = 4x + 5, y = 5 − x and 4y = x + 5.
Find the area of the region enclosed between the two curves x2 + y2 = 9 and (x − 3)2 + y2 = 9.
Using integration, find the area of the following region: \[\left\{ \left( x, y \right) : \frac{x^2}{9} + \frac{y^2}{4} \leq 1 \leq \frac{x}{3} + \frac{y}{2} \right\}\]
The area of the region formed by x2 + y2 − 6x − 4y + 12 ≤ 0, y ≤ x and x ≤ 5/2 is ______ .
The area of the region bounded by the parabola y = x2 + 1 and the straight line x + y = 3 is given by
The area bounded by the curve y2 = 8x and x2 = 8y is ___________ .
Area bounded by the curve y = x3, the x-axis and the ordinates x = −2 and x = 1 is ______.
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices area A(1, 2), B (2, 0) and C (4, 3).
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using vertical strips.
The area of the region bounded by the curve x = y2, y-axis and the line y = 3 and y = 4 is ______.
The area of the region bounded by the ellipse `x^2/25 + y^2/16` = 1 is ______.
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9` = 1.
Using integration, find the area of the region bounded by the curves x2 + y2 = 4, x = `sqrt(3)`y and x-axis lying in the first quadrant.
The area enclosed by y2 = 8x and y = `sqrt(2x)` that lies outside the triangle formed by y = `sqrt(2x)`, x = 1, y = `2sqrt(2)`, is equal to ______.
For real number a, b (a > b > 0),
let Area `{(x, y): x^2 + y^2 ≤ a^2 and x^2/a^2 + y^2/b^2 ≥ 1}` = 30π
Area `{(x, y): x^2 + y^2 ≥ b^2 and x^2/a^2 + y^2/b^2 ≤ 1}` = 18π.
Then the value of (a – b)2 is equal to ______.
Let the curve y = y(x) be the solution of the differential equation, `("dy")/("d"x) = 2(x + 1)`. If the numerical value of area bounded by the curve y = y(x) and x-axis is `(4sqrt(8))/3`, then the value of y(1) is equal to ______.
Let T be the tangent to the ellipse E: x2 + 4y2 = 5 at the point P(1, 1). If the area of the region bounded by the tangent T, ellipse E, lines x = 1 and x = `sqrt(5)` is `sqrt(5)`α + β + γ `cos^-1(1/sqrt(5))`, then |α + β + γ| is equal to ______.
Area (in sq.units) of the region outside `|x|/2 + |y|/3` = 1 and inside the ellipse `x^2/4 + y^2/9` = 1 is ______.
Let f(x) be a non-negative continuous function such that the area bounded by the curve y = f(x), x-axis and the ordinates x = `π/4` and x = `β > π/4` is `(βsinβ + π/4 cos β + sqrt(2)β)`. Then `f(π/2)` is ______.
Let a and b respectively be the points of local maximum and local minimum of the function f(x) = 2x3 – 3x2 – 12x. If A is the total area of the region bounded by y = f(x), the x-axis and the lines x = a and x = b, then 4A is equal to ______.
Using integration, find the area bounded by the curve y2 = 4ax and the line x = a.
