Advertisements
Advertisements
Question
Using integration, find the area of the region bounded by the curves x2 + y2 = 4, x = `sqrt(3)`y and x-axis lying in the first quadrant.
Solution
Given equation of circle x2 + y2 = 4
or x2 + y2 = (2)2
∴ Radius = 2
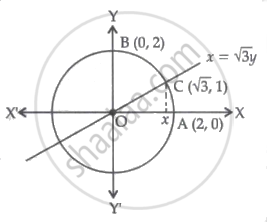
So, point A is (2, 0) and point B is (0, 2)
Let line x = `sqrt(3)`y intersect the circle at point C
On solving x2 + y2 = 4 and x = `sqrt(3)`y, we get
`(sqrt(3)y)^2 + y^2` = 4
⇒ 3y2 + y2 = 4
⇒ 4y2
⇒ y2 = 1
⇒ y = ±1
For y = 1, x = `sqrt(3)` and y = –1, x = `-sqrt(3)`
Since point C is in 1st quadrant
∴ C = `(sqrt(3), 1)`
∴ Required Area = `int_0^sqrt(3) y_"line" dx + int_sqrt(3)^2 y_"circle"dx`
= `int_0^sqrt(3) x/sqrt(3)dx + int_sqrt(3)^2 sqrt(4 - x^2)dx`
= `1/sqrt(3) int_0^sqrt(3) xdx + int_sqrt(3)^2 sqrt(4 - x^2)dx`
= `1/sqrt(3)[x^2/2]_0^sqrt(3) + [1/2xsqrt(4 - x^2) + (2)^2/2 sin^-1 x/2]_sqrt(3)^2`
= `1/(2sqrt(3)){(sqrt(3))^2 - 0} + [{1/2(2)sqrt(4 - 2^2) + 2sin^-1(2/2)} - {1/2(sqrt(3))sqrt(4 - (sqrt(3))^2) - 2sin^-1 sqrt(3)/2}]`
= `sqrt(3)/2 + 2sin^-1(1) - sqrt(3)/2 - 2sin^-1 sqrt(3)/2`
= `2 π/2 - 2 π/3`
= `π - (2π)/3`
= `π/3` sq.units
APPEARS IN
RELATED QUESTIONS
Find the area of the region bounded by the parabola y2 = 4ax and its latus rectum.
Find the area of the region bounded by the curve y = sinx, the lines x=-π/2 , x=π/2 and X-axis
Find the area of the region bounded by the curve x2 = 16y, lines y = 2, y = 6 and Y-axis lying in the first quadrant.
Find the area bounded by the curve y = sin x between x = 0 and x = 2π.
Sketch the graph of y = |x + 4|. Using integration, find the area of the region bounded by the curve y = |x + 4| and x = –6 and x = 0.
Make a rough sketch of the graph of the function y = 4 − x2, 0 ≤ x ≤ 2 and determine the area enclosed by the curve, the x-axis and the lines x = 0 and x = 2.
Find the area under the curve y = \[\sqrt{6x + 4}\] above x-axis from x = 0 to x = 2. Draw a sketch of curve also.
Find the area of the region bounded by x2 = 16y, y = 1, y = 4 and the y-axis in the first quadrant.
Find the area of the region common to the parabolas 4y2 = 9x and 3x2 = 16y.
Using integration, find the area of the triangular region, the equations of whose sides are y = 2x + 1, y = 3x+ 1 and x = 4.
Find the area, lying above x-axis and included between the circle x2 + y2 = 8x and the parabola y2 = 4x.
Prove that the area common to the two parabolas y = 2x2 and y = x2 + 4 is \[\frac{32}{3}\] sq. units.
Find the area of the region bounded by the curve y = \[\sqrt{1 - x^2}\], line y = x and the positive x-axis.
Find the area bounded by the lines y = 4x + 5, y = 5 − x and 4y = x + 5.
Find the area of the region {(x, y): x2 + y2 ≤ 4, x + y ≥ 2}.
Find the area enclosed by the parabolas y = 4x − x2 and y = x2 − x.
Find the area of the figure bounded by the curves y = | x − 1 | and y = 3 −| x |.
Find the area of the region bounded by the parabola y2 = 2x and the straight line x − y = 4.
The area included between the parabolas y2 = 4x and x2 = 4y is (in square units)
The ratio of the areas between the curves y = cos x and y = cos 2x and x-axis from x = 0 to x = π/3 is ________ .
The area bounded by the curve y = 4x − x2 and the x-axis is __________ .
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
Find the area of region bounded by the triangle whose vertices are (–1, 1), (0, 5) and (3, 2), using integration.
The area of the region bounded by the y-axis, y = cosx and y = sinx, 0 ≤ x ≤ `pi/2` is ______.
The area of the region bounded by the parabola (y – 2)2 = (x – 1), the tangent to it at the point whose ordinate is 3 and the x-axis is ______.
Find the area of the smaller region bounded by the curves `x^2/25 + y^2/16` = 1 and `x/5 + y/4` = 1, using integration.
Using integration, find the area bounded by the curve y2 = 4ax and the line x = a.
