Advertisements
Advertisements
Question
Find the area of the region bounded by curve 4x2 = y and the line y = 8x + 12, using integration.
Solution
Given curve is 4x2 = y and line is y = 8x + 12
On solving both equations, we get
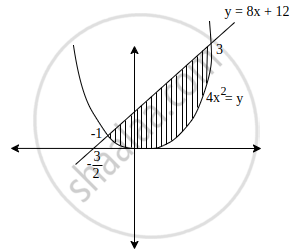
4x2 = 8x + 12
⇒ x2 = 2x + 3
⇒ x2 – 2x – 3 = 0
⇒ x = 3, –1
Required area = `int_-1^3 {(8x + 12) - 4x^2}dx`
= `4int_-1^3 (2x + 3 - x^2)dx`
= `4[x^2 + 3x - x^3/3]_-1^3`
= `4[(9 + 9 - 9) - (1 - 3 + 1/3)]`
= `4(9 + 2 - 1/3)`
= `4(11 - 1/3)`
= `4 xx 32/2`
= `128/2` sq.units
APPEARS IN
RELATED QUESTIONS
Find the area bounded by the curve y2 = 4ax, x-axis and the lines x = 0 and x = a.
Prove that the curves y2 = 4x and x2 = 4y divide the area of square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.
Find the area lying above the x-axis and under the parabola y = 4x − x2.
Find the area under the curve y = \[\sqrt{6x + 4}\] above x-axis from x = 0 to x = 2. Draw a sketch of curve also.
Using integration, find the area of the region bounded by the triangle ABC whose vertices A, B, C are (−1, 1), (0, 5) and (3, 2) respectively.
Find the area of the region included between the parabola y2 = x and the line x + y = 2.
Find the area bounded by the curves x = y2 and x = 3 − 2y2.
Using integration find the area of the region bounded by the curves \[y = \sqrt{4 - x^2}, x^2 + y^2 - 4x = 0\] and the x-axis.
If the area bounded by the parabola \[y^2 = 4ax\] and the line y = mx is \[\frac{a^2}{12}\] sq. units, then using integration, find the value of m.
Find the area of the region bounded by the parabola y2 = 2x and the straight line x − y = 4.
The area bounded by the curve y = x |x| and the ordinates x = −1 and x = 1 is given by
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices area A(1, 2), B (2, 0) and C (4, 3).
Find the equation of the parabola with latus-rectum joining points (4, 6) and (4, -2).
Find the area of the region bounded by the parabolas y2 = 6x and x2 = 6y.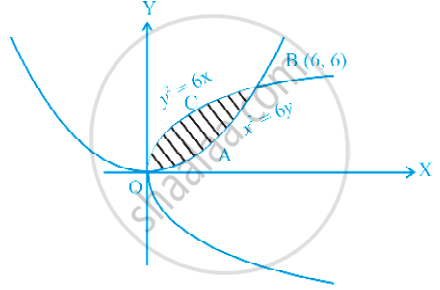
The area enclosed by the ellipse `x^2/"a"^2 + y^2/"b"^2` = 1 is equal to ______.
The area of the region bounded by the curve y = x2 and the line y = 16 ______.
Using integration, find the area of the region bounded by the line 2y = 5x + 7, x- axis and the lines x = 2 and x = 8.
Find the area enclosed by the curve y = –x2 and the straight lilne x + y + 2 = 0
The area of the region bounded by the curve x2 = 4y and the straight line x = 4y – 2 is ______.
The area of the region bounded by the ellipse `x^2/25 + y^2/16` = 1 is ______.
The area of the region bounded by the circle x2 + y2 = 1 is ______.
The region bounded by the curves `x = 1/2, x = 2, y = log x` and `y = 2^x`, then the area of this region, is
Find the area of the region bounded by `y^2 = 9x, x = 2, x = 4` and the `x`-axis in the first quadrant.
Find the area of the region bounded by the curve `y = x^2 + 2, y = x, x = 0` and `x = 3`
The area bounded by the curve `y = x|x|`, `x`-axis and the ordinate `x` = – 1 and `x` = 1 is given by
Using integration, find the area of the region bounded by the curves x2 + y2 = 4, x = `sqrt(3)`y and x-axis lying in the first quadrant.
Find the area of the smaller region bounded by the curves `x^2/25 + y^2/16` = 1 and `x/5 + y/4` = 1, using integration.
Using integration, find the area bounded by the curve y2 = 4ax and the line x = a.
