Question

Find the area bounded by the curves x = y² and x = 3 − 2y².

Answer 1

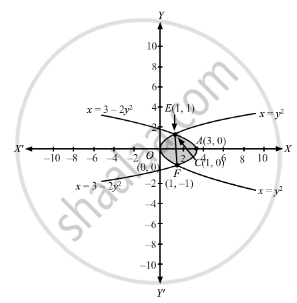
 x = y² is a parabola opening towards positive x-axis , having vertex at O (0,0) and symmetrical about x-axis
 x = 3 − 2y² is a parabola opening negative x-axis, having vertex at A (3, 0) and symmetrical about x-axis, cutting y-axis at B and B'

Solving the two equations for the point of intersection of two parabolas
\[x = y^2 \]
\[x = 3 - 2 y^2 \]
\[ \Rightarrow y^2 = 3 - 2 y^2 \]
\[ \Rightarrow 3 y^2 = 3\]
\[ \Rightarrow y = \pm 1\]
\[y = 1 , \Rightarrow x = 1\text{ and }y = - 1 \Rightarrow x = 1\]
\[ \Rightarrow E\left( 1, 1 \right)\text{ and }F\left( 1, - 1 \right)\text{ are two points of intersection . }\]
\[\text{ The curve character changes at E and F . }\]
\[\text{ Draw EF parallel to y - axis . }\]
\[C(1, 0)\text{ is the point of intersection of EF ith }x -\text{ axis }\]
\[\text{ Since both curves are symmetrical about } x - \text{ axis }, \]
\[\text{ Area of shaded region OEAFO }= 2\text{ Area OEAO }\hspace{0.167em} \]
\[ = 2\left(\text{ Area OECO + area CEAC }\right) . . . . . \left( 1 \right)\]
\[\text{ Area OECO }= \int_o^1 \left| y_1 \right| dx ............\left\{\text{ where }P\left( x, y_1 \right)\text{ is a point on }x = y^2 \right\}\]
\[ = \int_o^1 y_1 dx ............\left\{ \text{ as }y_1 > 0 \right\}\]
\[ = \int_o^1 \sqrt{x} dx\]
\[ = \left[ \frac{x^\frac{3}{2}}{\frac{3}{2}} \right]_0^1 \]
\[ = \frac{2}{3}\text{ sq units .} . . . . \left( 2 \right)\]
\[\text{ area CEAC }= \int_1^3 \left| y_2 \right| dx ...........\left\{\text{ where }Q\left( x, y_2 \right)\text{ is a point on }x = 3 - 2 y^2 \right\}\]
\[ = \int_1^3 y_2 dx ............\left\{\text{ as }y_2 > 0 \right\}\]
\[ = \int_1^3 \sqrt{\frac{3 - x}{2}}dx\]
\[ = \frac{1}{\sqrt{2}} \int_1^3 \sqrt{3 - x} dx\]
\[ = \frac{1}{\sqrt{2}} \left[ - \frac{\left( 3 - x \right)^\frac{3}{2}}{\frac{3}{2}} \right]_1^3 \]
\[ = \frac{1}{\sqrt{2}} \times \frac{2}{3}\left[ 0 + 2^\frac{3}{2} \right]\]
\[ = \frac{2 \times 2\sqrt{2}}{\sqrt{2} \times 3} = \frac{4}{3}\text{ sq . units }. . . . . \left( 3 \right)\]
\[\text{ From }\left( 1 \right), \left( 2 \right)\text{ and }\left( 3 \right), \text{ we get }\]
\[ \text{ Therefore, area of Shaded region OEAFO }= 2\left[ \frac{2}{3} + \frac{4}{3} \right] = 2 \times 2 = 4\text{ sq units }\]