Advertisements
Advertisements
Question
Using integration, find the area of the region bounded between the line x = 4 and the parabola y2 = 16x.
Solution
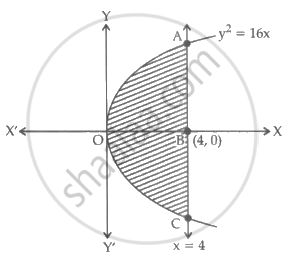
The shaded region OACO is the region bounded by the parabola y2 = 16x and the line x = 4.
The area OACO is symmetrical about X-axis.
Area of OACO = 2(Area of OAB)
= `2 int_0^4 "y dx"`
= `2 int_0^4 4sqrt"x" "dx"`
= `8 xx 2/3 ["x"^(3//2)]_0^4`
= `16/3 (4)^(3//2)`
= `16/3 xx 8`
= `128/3`
So, the required area is `128/3` sq. units.
APPEARS IN
RELATED QUESTIONS
Find the area of the region bounded by the parabola y2 = 16x and the line x = 3.
Find the area of the region common to the circle x2 + y2 =9 and the parabola y2 =8x
Find the area of the sector of a circle bounded by the circle x2 + y2 = 16 and the line y = x in the ftrst quadrant.
Find the area of the region bounded by the curve x2 = 16y, lines y = 2, y = 6 and Y-axis lying in the first quadrant.
Sketch the graph of y = |x + 4|. Using integration, find the area of the region bounded by the curve y = |x + 4| and x = –6 and x = 0.
Show that the areas under the curves y = sin x and y = sin 2x between x = 0 and x =\[\frac{\pi}{3}\] are in the ratio 2 : 3.
Find the area of the region \[\left\{ \left( x, y \right): \frac{x^2}{a^2} + \frac{y^2}{b^2} \leq 1 \leq \frac{x}{a} + \frac{y}{b} \right\}\]
Prove that the area in the first quadrant enclosed by the x-axis, the line x = \[\sqrt{3}y\] and the circle x2 + y2 = 4 is π/3.
Using integration find the area of the region:
\[\left\{ \left( x, y \right) : \left| x - 1 \right| \leq y \leq \sqrt{5 - x^2} \right\}\]
Find the area of the circle x2 + y2 = 16 which is exterior to the parabola y2 = 6x.
Find the area of the figure bounded by the curves y = | x − 1 | and y = 3 −| x |.
Find the area bounded by the parabola x = 8 + 2y − y2; the y-axis and the lines y = −1 and y = 3.
The area bounded by the parabola y2 = 4ax and x2 = 4ay is ___________ .
The closed area made by the parabola y = 2x2 and y = x2 + 4 is __________ .
The area bounded by the curve y2 = 8x and x2 = 8y is ___________ .
Using integration, find the area of the region bounded by the line x – y + 2 = 0, the curve x = \[\sqrt{y}\] and y-axis.
Find the area of the region bounded by the parabola y2 = 2x and the straight line x – y = 4.
The area enclosed by the circle x2 + y2 = 2 is equal to ______.
Find the area of the region bounded by the curve y2 = 4x, x2 = 4y.
Find the area of the region bounded by the curve y2 = 2x and x2 + y2 = 4x.
Find the area bounded by the curve y = sinx between x = 0 and x = 2π.
Area of the region bounded by the curve y = cosx between x = 0 and x = π is ______.
Using integration, find the area of the region in the first quadrant enclosed by the line x + y = 2, the parabola y2 = x and the x-axis.
Using integration, find the area of the region `{(x, y): 0 ≤ y ≤ sqrt(3)x, x^2 + y^2 ≤ 4}`
Area of the region bounded by the curve y = |x + 1| + 1, x = –3, x = 3 and y = 0 is
Find the area of the region bounded by `y^2 = 9x, x = 2, x = 4` and the `x`-axis in the first quadrant.
The area of the region S = {(x, y): 3x2 ≤ 4y ≤ 6x + 24} is ______.
The area (in sq.units) of the region A = {(x, y) ∈ R × R/0 ≤ x ≤ 3, 0 ≤ y ≤ 4, y ≤x2 + 3x} is ______.
Evaluate:
`int_0^1x^2dx`
