Advertisements
Advertisements
Question
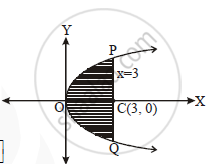
Find the area of the region bounded by the parabola y2 = 16x and the line x = 3.
Solution
`y^2 = 16x`
`area =2int_0^3ydx`
`=2int_0^34 sqrtxdx`
`=8 2/3[x^(3/2)]_0^3`
`=16/3[3^(3/2)]`
`=16/3[3xx3^(1/2)]`
`=16[3^(1/2)]`
`=16sqrt3 sq.units`
APPEARS IN
RELATED QUESTIONS
Find the area of the region common to the circle x2 + y2 =9 and the parabola y2 =8x
Find the area of the sector of a circle bounded by the circle x2 + y2 = 16 and the line y = x in the ftrst quadrant.
Find the area bounded by the curve y = sin x between x = 0 and x = 2π.
Find the area of the region lying in the first quandrant bounded by the curve y2= 4x, X axis and the lines x = 1, x = 4
Find the area lying above the x-axis and under the parabola y = 4x − x2.
Draw a rough sketch to indicate the region bounded between the curve y2 = 4x and the line x = 3. Also, find the area of this region.
Find the area under the curve y = \[\sqrt{6x + 4}\] above x-axis from x = 0 to x = 2. Draw a sketch of curve also.
Determine the area under the curve y = \[\sqrt{a^2 - x^2}\] included between the lines x = 0 and x = a.
Using integration, find the area of the region bounded by the triangle whose vertices are (2, 1), (3, 4) and (5, 2).
Draw a rough sketch of the region {(x, y) : y2 ≤ 3x, 3x2 + 3y2 ≤ 16} and find the area enclosed by the region using method of integration.
Draw a rough sketch and find the area of the region bounded by the two parabolas y2 = 4x and x2 = 4y by using methods of integration.
Find the area of the region bounded by \[y = \sqrt{x}\] and y = x.
Using integration, find the area of the triangle ABC coordinates of whose vertices are A (4, 1), B (6, 6) and C (8, 4).
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2.
Find the area of the region bounded by the curve y = \[\sqrt{1 - x^2}\], line y = x and the positive x-axis.
Find the area of the region enclosed between the two curves x2 + y2 = 9 and (x − 3)2 + y2 = 9.
Find the area enclosed by the curves 3x2 + 5y = 32 and y = | x − 2 |.
In what ratio does the x-axis divide the area of the region bounded by the parabolas y = 4x − x2 and y = x2− x?
If the area enclosed by the parabolas y2 = 16ax and x2 = 16ay, a > 0 is \[\frac{1024}{3}\] square units, find the value of a.
The area bounded by the curve y = loge x and x-axis and the straight line x = e is ___________ .
Area bounded by parabola y2 = x and straight line 2y = x is _________ .
The area of the circle x2 + y2 = 16 enterior to the parabola y2 = 6x is
Find the equation of the parabola with latus-rectum joining points (4, 6) and (4, -2).
Sketch the graphs of the curves y2 = x and y2 = 4 – 3x and find the area enclosed between them.
Using the method of integration, find the area of the region bounded by the lines 3x − 2y + 1 = 0, 2x + 3y − 21 = 0 and x − 5y + 9 = 0
Find the area of the region bounded by the curves y2 = 9x, y = 3x
Find the area enclosed by the curve y = –x2 and the straight lilne x + y + 2 = 0
Find the area of region bounded by the triangle whose vertices are (–1, 1), (0, 5) and (3, 2), using integration.
Compute the area bounded by the lines x + 2y = 2, y – x = 1 and 2x + y = 7.
Find the area bounded by the curve y = 2cosx and the x-axis from x = 0 to x = 2π
The area of the region bounded by the curve x2 = 4y and the straight line x = 4y – 2 is ______.
Let f(x) be a continuous function such that the area bounded by the curve y = f(x), x-axis and the lines x = 0 and x = a is `a^2/2 + a/2 sin a + pi/2 cos a`, then `f(pi/2)` =
Area of the region bounded by the curve y = |x + 1| + 1, x = –3, x = 3 and y = 0 is
Find the area of the region bounded by `x^2 = 4y, y = 2, y = 4`, and the `y`-axis in the first quadrant.
What is the area of the region bounded by the curve `y^2 = 4x` and the line `x` = 3.
The area bounded by the curve `y = x^3`, the `x`-axis and ordinates `x` = – 2 and `x` = 1
Find the area bounded by the curve y = |x – 1| and y = 1, using integration.
The area (in sq.units) of the region A = {(x, y) ∈ R × R/0 ≤ x ≤ 3, 0 ≤ y ≤ 4, y ≤x2 + 3x} is ______.
Let g(x) = cosx2, f(x) = `sqrt(x)`, and α, β (α < β) be the roots of the quadratic equation 18x2 – 9πx + π2 = 0. Then the area (in sq. units) bounded by the curve y = (gof)(x) and the lines x = α, x = β and y = 0, is ______.
Find the area of the smaller region bounded by the curves `x^2/25 + y^2/16` = 1 and `x/5 + y/4` = 1, using integration.
