Advertisements
Advertisements
Question
Find the area enclosed by the curve y = –x2 and the straight lilne x + y + 2 = 0
Solution
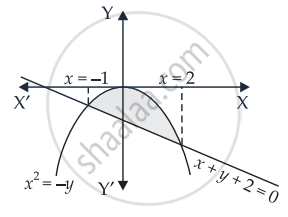
We are given that y = –x2 or x2 = –y
And the line x + y + 2 = 0
Solving the two equations,
We get x – x2 + 2 = 0
⇒ x2 – x – 2 = 0
⇒ x2 – 2x + x – 2 = 0
⇒ x(x – 2) + 1(x – 2) = 0
⇒ (x – 2)(x + 1) = 0
∴ x = –1, 2
Area of the required shaded region
= `|int_-1^2 (-x - 2) "d"x - int_-1^2 - x^2 "d"x|`
⇒ `|-[x^2/2 + x]_-1^2 + 1/3 [x^3]_-1^2|`
⇒ `|-[4/2 + 4) - (1/2 - 2)] + 1/3(8 + 1)|`
⇒ `|-(6 + 3/2) + 1/3(9)|`
⇒ `|- 15/2 + 3|`
⇒ `|(-15 + 6)/2| = |(-9)/2|`
= `9/2` sq.units
APPEARS IN
RELATED QUESTIONS
Find the area of the region common to the circle x2 + y2 =9 and the parabola y2 =8x
Find the area of the region lying in the first quandrant bounded by the curve y2= 4x, X axis and the lines x = 1, x = 4
Find the area of ellipse `x^2/1 + y^2/4 = 1`
Using integration, find the area of the region bounded by the line 2y = 5x + 7, x-axis and the lines x = 2 and x = 8.
Find the area of the region bounded by the curve xy − 3x − 2y − 10 = 0, x-axis and the lines x = 3, x = 4.
Find the area bounded by the ellipse \[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\] and the ordinates x = ae and x = 0, where b2 = a2 (1 − e2) and e < 1.
Using integration, find the area of the region bounded by the triangle ABC whose vertices A, B, C are (−1, 1), (0, 5) and (3, 2) respectively.
Find the area of the region bounded by \[y = \sqrt{x}, x = 2y + 3\] in the first quadrant and x-axis.
Find the area common to the circle x2 + y2 = 16 a2 and the parabola y2 = 6 ax.
OR
Find the area of the region {(x, y) : y2 ≤ 6ax} and {(x, y) : x2 + y2 ≤ 16a2}.
Using integration, find the area of the region bounded by the triangle whose vertices are (−1, 2), (1, 5) and (3, 4).
Find the area of the region bounded by the parabola y2 = 2x + 1 and the line x − y − 1 = 0.
Find the area of the circle x2 + y2 = 16 which is exterior to the parabola y2 = 6x.
Find the area enclosed by the parabolas y = 4x − x2 and y = x2 − x.
Find the area of the figure bounded by the curves y = | x − 1 | and y = 3 −| x |.
If the area above the x-axis, bounded by the curves y = 2kx and x = 0, and x = 2 is \[\frac{3}{\log_e 2}\], then the value of k is __________ .
The closed area made by the parabola y = 2x2 and y = x2 + 4 is __________ .
Area bounded by parabola y2 = x and straight line 2y = x is _________ .
The area of the region (in square units) bounded by the curve x2 = 4y, line x = 2 and x-axis is
Using integration, find the area of the smaller region bounded by the ellipse `"x"^2/9+"y"^2/4=1`and the line `"x"/3+"y"/2=1.`
Find the area of the region bounded by y = `sqrt(x)` and y = x.
Find the area bounded by the curve y = sinx between x = 0 and x = 2π.
Find the area bounded by the lines y = 4x + 5, y = 5 – x and 4y = x + 5.
Using integration, find the area of the region `{(x, y): 0 ≤ y ≤ sqrt(3)x, x^2 + y^2 ≤ 4}`
If a and c are positive real numbers and the ellipse `x^2/(4c^2) + y^2/c^2` = 1 has four distinct points in common with the circle `x^2 + y^2 = 9a^2`, then
The area of the region enclosed by the parabola x2 = y, the line y = x + 2 and the x-axis, is
Find the area of the region bounded by the curve `y^2 - x` and the line `x` = 1, `x` = 4 and the `x`-axis.
The area enclosed by y2 = 8x and y = `sqrt(2x)` that lies outside the triangle formed by y = `sqrt(2x)`, x = 1, y = `2sqrt(2)`, is equal to ______.
Using integration, find the area bounded by the curve y2 = 4ax and the line x = a.
