Question

Find the area of the region bounded by \[y = \sqrt{x}, x = 2y + 3\]  in the first quadrant and x-axis.

Answer 1

The curve \[y = \sqrt{x}\]  or  \[y^2 = x\] represents the parabola opening towards the positive x-axis.

The curve x = 2y + 3 represents a line passing through (3, 0) and \[\left( 0, - \frac{3}{2} \right)\]
Solving \[y^2 = x\] and x = 2y + 3, we get
\[y^2 = 2y + 3\]
\[ \Rightarrow y^2 - 2y - 3 = 0\]
\[ \Rightarrow \left( y - 3 \right)\left( y + 1 \right) = 0\]
\[ \Rightarrow y = 3\text{ or }y = - 1\]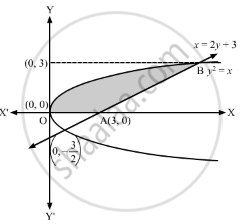

∴ Required area = Area of the shaded region

\[= \int_0^3 x_{\text{ line }} dy - \int_0^3 x_{\text{ parabola }} dy\]

\[ = \int_0^3 \left( 2y + 3 \right)dy - \int_0^3 y^2 dy\]

\[ = \left.\frac{\left( 2y + 3 \right)^2}{2 \times 2}\right|_0^3 - \left.\frac{y^3}{3}\right|_0^3 \]

\[ = \frac{1}{4}\left[ \left( 2 \times 3 + 3 \right)^2 - 3^2 \right] - \frac{1}{3}\left( 3^3 - 0 \right)\]

\[ = \frac{1}{4}\left( 81 - 9 \right) - \frac{1}{3}\left( 27 - 0 \right)\]

\[ = 18 - 9\]

\[ = 9\text{ square units }\]