Advertisements
Advertisements
Question
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices area A(1, 2), B (2, 0) and C (4, 3).
Solution

Let A(1, 2), B (2, 0) and C (4, 3) be the vertices of a triangle ABC
\[\text { Area of } \bigtriangleup ABC = \text { Area of trapezium } ADEC - \text { Area of } \bigtriangleup ADB - \text { Area of } \bigtriangleup CBE\]
\[\text { Equation of sides AC, AB and BC are given by }: \]
\[y = \frac{x}{3} + \frac{5}{3}, y = - 2x + 4 \text { and } y = \frac{3x}{2} - 3 \text {P respectively }\]
\[\text { Hence, area of } \bigtriangleup ABC = \int_1^4 \left( \frac{x}{3} + \frac{5}{3} \right)dx - \int_1^2 \left( - 2x + 4 \right)dx - \int_2^4 \left( \frac{3}{2}x - 3 \right)dx\]
\[ = \frac{1}{3} \left[ \frac{x^2}{2} + 5x \right]_1^4 - \left[ - \frac{2 x^2}{2} + 4x \right]_1^2 - \left[ \frac{3}{4} x^2 - 3x \right]_2^4 \]
\[ = \frac{1}{3}\left[ \left( \frac{16}{2} + 20 \right) - \left( \frac{1}{2} + 5 \right) \right] - \left[ \left( - 4 + 8 \right) - \left( - 1 + 4 \right) \right] - \left[ \left( 12 - 12 \right) - \left( 3 - 6 \right) \right]\]
\[ = \frac{1}{3}\left[ 28 - \frac{11}{2} \right] - \left[ 4 - 3 \right] - \left[ 0 + 3 \right]\]
\[ = \frac{1}{3}\left[ \frac{45}{2} \right] - \left[ 1 \right] - \left[ 3 \right]\]
\[ = \frac{7}{2}\]
APPEARS IN
RELATED QUESTIONS
Find the area bounded by the curve y2 = 4ax, x-axis and the lines x = 0 and x = a.
triangle bounded by the lines y = 0, y = x and x = 4 is revolved about the X-axis. Find the volume of the solid of revolution.
Draw a rough sketch of the curve y = \[\frac{\pi}{2} + 2 \sin^2 x\] and find the area between x-axis, the curve and the ordinates x = 0, x = π.
Find the area bounded by the curve y = cos x, x-axis and the ordinates x = 0 and x = 2π.
Compare the areas under the curves y = cos2 x and y = sin2 x between x = 0 and x = π.
Calculate the area of the region bounded by the parabolas y2 = x and x2 = y.
Find the area of the region common to the parabolas 4y2 = 9x and 3x2 = 16y.
Find the area of the region \[\left\{ \left( x, y \right): \frac{x^2}{a^2} + \frac{y^2}{b^2} \leq 1 \leq \frac{x}{a} + \frac{y}{b} \right\}\]
Using integration, find the area of the triangular region, the equations of whose sides are y = 2x + 1, y = 3x+ 1 and x = 4.
Draw a rough sketch of the region {(x, y) : y2 ≤ 3x, 3x2 + 3y2 ≤ 16} and find the area enclosed by the region using method of integration.
Find the area of the region bounded by the curves y = x − 1 and (y − 1)2 = 4 (x + 1).
Using integration find the area of the region:
\[\left\{ \left( x, y \right) : \left| x - 1 \right| \leq y \leq \sqrt{5 - x^2} \right\}\]
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2= 32.
Find the area enclosed by the parabolas y = 4x − x2 and y = x2 − x.
Find the area of the region bounded by the parabola y2 = 2x and the straight line x − y = 4.
The area bounded by the parabola x = 4 − y2 and y-axis, in square units, is ____________ .
The area bounded by the curve y = f (x), x-axis, and the ordinates x = 1 and x = b is (b −1) sin (3b + 4). Then, f (x) is __________ .
Using integration, find the area of the region bounded by the line x – y + 2 = 0, the curve x = \[\sqrt{y}\] and y-axis.
Sketch the graphs of the curves y2 = x and y2 = 4 – 3x and find the area enclosed between them.
Find the area of the region bound by the curves y = 6x – x2 and y = x2 – 2x
Using integration, find the area of the smaller region bounded by the ellipse `"x"^2/9+"y"^2/4=1`and the line `"x"/3+"y"/2=1.`
Find the area of the region bounded by the parabolas y2 = 6x and x2 = 6y.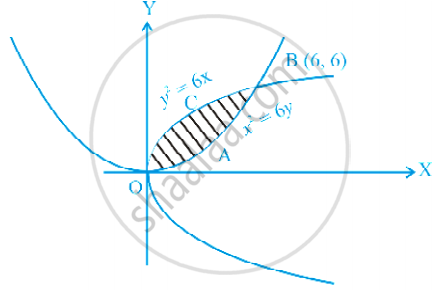
Find the area of region bounded by the line x = 2 and the parabola y2 = 8x
Find the area bounded by the lines y = 4x + 5, y = 5 – x and 4y = x + 5.
Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32 is ______.
Using integration, find the area of the region in the first quadrant enclosed by the line x + y = 2, the parabola y2 = x and the x-axis.
The area of the region enclosed by the parabola x2 = y, the line y = x + 2 and the x-axis, is
Let f : [–2, 3] `rightarrow` [0, ∞) be a continuous function such that f(1 – x) = f(x) for all x ∈ [–2, 3]. If R1 is the numerical value of the area of the region bounded by y = f(x), x = –2, x = 3 and the axis of x and R2 = `int_-2^3 xf(x)dx`, then ______.
