Advertisements
Advertisements
Question
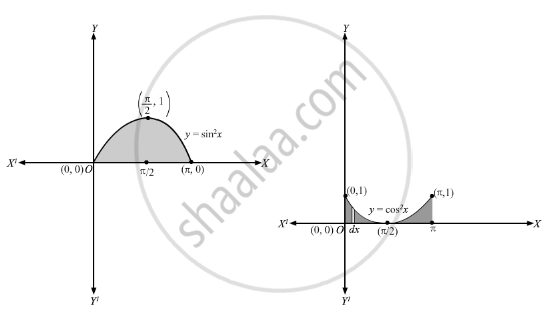
Compare the areas under the curves y = cos2 x and y = sin2 x between x = 0 and x = π.
Solution
|
X |
0 | \[\frac{\pi}{4}\] |
\[\frac{\pi}{3}\]
|
\[\frac{\pi}{2}\]
|
\[\frac{2\pi}{3}\]
|
\[\frac{5\pi}{6}\]
|
\[\pi\]
|
|
\[y = \cos^2 x\]
|
1 | 0.5 | 0.25 | 0 | 0.25 | 0.75 | 1 |
|
\[y = \sin^2 x\]
|
0 | 0.5 | 0.75 | 1 | 0.75 | 0.25 | 0 |
Let A1 be the area of curve \[y = \cos^2 x\text{ between }x = 0 \text{ and }x = \pi\]
Let A2 be the area of curve \[y = \sin^2 x \text{ between }x = 0\text{ and }x = \pi\]
Consider, a vertical strip of length \[= \left| y \right|\] and width \[= dx\] in the shaded region of both the curves
The area of approximating rectangle \[= \left| y \right| dx\]
\[\text{The approximating rectangle moves from}x = 0\text{ to }x = \pi\]
\[ A_1 = \int_0^\pi \left| y \right| dx\]
\[ \Rightarrow A_1 = \int_0^\pi y dx ..................\left[ 0 \leq x \leq \pi , y > 0 \Rightarrow \left| y \right| = y \right]\]
\[ \Rightarrow A_1 = \int_0^\pi \cos^2 x dx\]
\[ \Rightarrow A_1 = \int_0^\pi \left( 1 + cos 2x \right) dx .................\left[ \cos^2 x = \left( 1 + \cos 2x \right) \right]\]
\[ \Rightarrow A_1 = \frac{1}{2} \left[ x + \frac{\sin 2x}{2} \right]_0^\pi \]
\[ \Rightarrow A_1 = \frac{1}{2}\left[ \pi + \frac{\sin 2\pi}{2} - 0 \right]\]
\[ \Rightarrow A_1 = \frac{\pi}{2} \text{ Sq . units }\]
Also,
\[ A_2 = \int_0^\pi \left| y \right| dx\]
\[ \Rightarrow A_2 = \int_0^\pi y dx .................\left[ 0 \leq x \leq \pi , y > 0 \Rightarrow \left| y \right| = y \right]\]
\[ \Rightarrow A_2 = \int_0^\pi \sin^2 x dx\]
\[ \Rightarrow A_2 = \left[ \frac{x}{2} - \frac{1}{2}\frac{\sin 2x}{2} \right]_0^\pi \]
\[ \Rightarrow A_2 = \frac{\pi}{2} - \left( \frac{1}{2}\frac{\sin 2\pi}{2} \right)\]
\[ \Rightarrow A_2 = \frac{\pi}{2} sq . units\]
\[ \therefore\text{ Area of curves }y = \cos^2 x\text{ and area of curve }y = \sin^2 x \text{ are both equal to }\frac{\pi}{2}\text{ sq . units }\]
APPEARS IN
RELATED QUESTIONS
Using integration, find the area bounded by the curve x2 = 4y and the line x = 4y − 2.
Find the area of the region bounded by the curve x2 = 16y, lines y = 2, y = 6 and Y-axis lying in the first quadrant.
Draw the rough sketch of y2 + 1 = x, x ≤ 2. Find the area enclosed by the curve and the line x = 2.
Find the area of the region bounded by the curve \[x = a t^2 , y = 2\text{ at }\]between the ordinates corresponding t = 1 and t = 2.
Find the area of the region bounded by y =\[\sqrt{x}\] and y = x.
Using integration, find the area of the region bounded by the triangle whose vertices are (2, 1), (3, 4) and (5, 2).
Using integration, find the area of the region bounded by the triangle ABC whose vertices A, B, C are (−1, 1), (0, 5) and (3, 2) respectively.
Find the area of the region common to the circle x2 + y2 = 16 and the parabola y2 = 6x.
Draw a rough sketch of the region {(x, y) : y2 ≤ 5x, 5x2 + 5y2 ≤ 36} and find the area enclosed by the region using method of integration.
Find the area of the region bounded by \[y = \sqrt{x}, x = 2y + 3\] in the first quadrant and x-axis.
Find the area enclosed by the parabolas y = 5x2 and y = 2x2 + 9.
Find the area of the region bounded by the curves y = x − 1 and (y − 1)2 = 4 (x + 1).
Find the area enclosed by the curve \[y = - x^2\] and the straight line x + y + 2 = 0.
Using integration, find the area of the triangle ABC coordinates of whose vertices are A (4, 1), B (6, 6) and C (8, 4).
Find the area of the region bounded by the curve y = \[\sqrt{1 - x^2}\], line y = x and the positive x-axis.
Find the area of the region between the parabola x = 4y − y2 and the line x = 2y − 3.
The area bounded by the curve y = loge x and x-axis and the straight line x = e is ___________ .
The area bounded by the parabola x = 4 − y2 and y-axis, in square units, is ____________ .
The area of the region bounded by the parabola y = x2 + 1 and the straight line x + y = 3 is given by
The area bounded by the parabola y2 = 8x, the x-axis and the latusrectum is ___________ .
The area bounded by the curve y = x |x| and the ordinates x = −1 and x = 1 is given by
The area of the circle x2 + y2 = 16 enterior to the parabola y2 = 6x is
Area of the region bounded by the curve y2 = 4x, y-axis and the line y = 3, is
Find the coordinates of a point of the parabola y = x2 + 7x + 2 which is closest to the straight line y = 3x − 3.
Find the area of the region bounded by the curve y = x3 and y = x + 6 and x = 0
Find the area of the region included between y2 = 9x and y = x
Find the area of region bounded by the line x = 2 and the parabola y2 = 8x
Sketch the region `{(x, 0) : y = sqrt(4 - x^2)}` and x-axis. Find the area of the region using integration.
The area of the region bounded by the curve y = `sqrt(16 - x^2)` and x-axis is ______.
Area of the region bounded by the curve y = cosx between x = 0 and x = π is ______.
Using integration, find the area of the region bounded between the line x = 4 and the parabola y2 = 16x.
The area of the region enclosed by the parabola x2 = y, the line y = x + 2 and the x-axis, is
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9` = 1.
Using integration, find the area of the region bounded by the curves x2 + y2 = 4, x = `sqrt(3)`y and x-axis lying in the first quadrant.
For real number a, b (a > b > 0),
let Area `{(x, y): x^2 + y^2 ≤ a^2 and x^2/a^2 + y^2/b^2 ≥ 1}` = 30π
Area `{(x, y): x^2 + y^2 ≥ b^2 and x^2/a^2 + y^2/b^2 ≤ 1}` = 18π.
Then the value of (a – b)2 is equal to ______.
Let f(x) be a non-negative continuous function such that the area bounded by the curve y = f(x), x-axis and the ordinates x = `π/4` and x = `β > π/4` is `(βsinβ + π/4 cos β + sqrt(2)β)`. Then `f(π/2)` is ______.
Find the area of the following region using integration ((x, y) : y2 ≤ 2x and y ≥ x – 4).
Find the area of the minor segment of the circle x2 + y2 = 4 cut off by the line x = 1, using integration.
