Advertisements
Advertisements
Question
Sketch the region `{(x, 0) : y = sqrt(4 - x^2)}` and x-axis. Find the area of the region using integration.
Solution
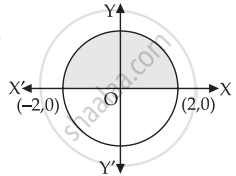
Given that `{(x, 0) : y = sqrt(4 - x^2)}`
⇒ y2 = 4 – x2
⇒ x2 + y2 = 4 which is a circle.
Required area = `2 * int_0^2 sqrt(4 - x^2) "d"x`
Since circle is symmetrical about y-axis
= `2 * int_0^2 sqrt((2)^2 - x^2) "d"x`
= `2 * [x/2 sqrt(4 - x^2) + 4/2 sin^-1 x/2]_0^2`
= `2[(2/2 sqrt(4 - 4) + 2 sin^-1 (1)) - (0 + 0)]`
= `2[2 * pi/2]`
= 2π sq.units
Hence, the required area = 2π sq.units
APPEARS IN
RELATED QUESTIONS
triangle bounded by the lines y = 0, y = x and x = 4 is revolved about the X-axis. Find the volume of the solid of revolution.
Sketch the graph of y = |x + 4|. Using integration, find the area of the region bounded by the curve y = |x + 4| and x = –6 and x = 0.
Using integration, find the area of the region bounded between the line x = 2 and the parabola y2 = 8x.
Using integration, find the area of the region bounded by the line y − 1 = x, the x − axis and the ordinates x= −2 and x = 3.
Sketch the graph y = | x + 3 |. Evaluate \[\int\limits_{- 6}^0 \left| x + 3 \right| dx\]. What does this integral represent on the graph?
Calculate the area of the region bounded by the parabolas y2 = x and x2 = y.
Find the area of the region common to the parabolas 4y2 = 9x and 3x2 = 16y.
Find the area of the region \[\left\{ \left( x, y \right): \frac{x^2}{a^2} + \frac{y^2}{b^2} \leq 1 \leq \frac{x}{a} + \frac{y}{b} \right\}\]
Find the area of the region bounded by the curves y = x − 1 and (y − 1)2 = 4 (x + 1).
Using integration, find the area of the triangle ABC coordinates of whose vertices are A (4, 1), B (6, 6) and C (8, 4).
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2= 32.
Find the area of the circle x2 + y2 = 16 which is exterior to the parabola y2 = 6x.
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using horizontal strips.
Area bounded by the curve y = x3, the x-axis and the ordinates x = −2 and x = 1 is ______.
Area lying in first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2, is
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices area A(1, 2), B (2, 0) and C (4, 3).
Using integration, find the area of the region bounded by the parabola y2 = 4x and the circle 4x2 + 4y2 = 9.
Find the area of the region bounded by the parabola y2 = 2px, x2 = 2py
Find the area of the region bounded by the curve y = x3 and y = x + 6 and x = 0
Find the area of region bounded by the triangle whose vertices are (–1, 1), (0, 5) and (3, 2), using integration.
The area of the region bounded by the curve y = sinx between the ordinates x = 0, x = `pi/2` and the x-axis is ______.
The area of the region bounded by the circle x2 + y2 = 1 is ______.
Using integration, find the area of the region in the first quadrant enclosed by the line x + y = 2, the parabola y2 = x and the x-axis.
Find the area of the region bounded by `y^2 = 9x, x = 2, x = 4` and the `x`-axis in the first quadrant.
Smaller area bounded by the circle `x^2 + y^2 = 4` and the line `x + y = 2` is.
The area (in square units) of the region bounded by the curves y + 2x2 = 0 and y + 3x2 = 1, is equal to ______.
Find the area of the following region using integration ((x, y) : y2 ≤ 2x and y ≥ x – 4).
Find the area of the region bounded by the curve x2 = 4y and the line x = 4y – 2.
