Advertisements
Advertisements
Question
Using integration, find the area of the region bounded by the line y − 1 = x, the x − axis and the ordinates x= −2 and x = 3.
Solution
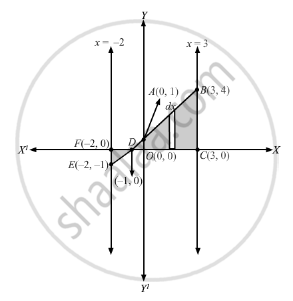
\[\because y - 1 = x\text{ is a straight line cutting x - axis at D( - 1, 0) and y - axis at A( 0, 1) }\]
\[\text{ And, }x = - 2\text{ and }x = 3 \text{ are straight lines parallel to y - axis }\]
\[\text{ Also, since }\left| y \right| = - \left( 1 + x \right),\text{ for } x \leq - 1\]
\[\text{ And }\left| y \right| = \left( 1 + x \right), x > - 1\]
\[ \therefore\text{ Area of region bound by line }y - 1 = x , x \text{ axis and the ordinates } x = - 2\text{ and }x = 3\text{ is }\]
\[\text{ Area A = area FED + area DOA + area OABC }\]
\[ \Rightarrow A = \int_{- 2}^3 \left| y \right| dx\]
\[ \Rightarrow A = \int_{- 2}^{- 1} \left| y \right| dx + \int_{- 1}^0 \left| y \right| dx + \int_0^3 \left| y \right| dx\]
\[ \Rightarrow A = \int_{- 2}^{- 1} - \left( 1 + x \right) dx + \int_{- 1}^0 \left( 1 + x \right) dx + \int_0^3 \left( 1 + x \right) dx\]
\[ \Rightarrow A = - \left[ x + \frac{x^2}{2} \right]_{- 2}^{- 1} + \left[ x + \frac{x^2}{2} \right]_{- 1}^0 + \left[ x + \frac{x^2}{2} \right]_0^3 \]
\[ \Rightarrow A = \left[ 1 - \frac{1}{2} - 2 + \frac{4}{2} \right] + \left[ 0 + 1 - \frac{1}{2} \right] + \left[ 3 + \frac{9}{2} \right]\]
\[ \Rightarrow A = - 1 + \frac{3}{2} + 1 - \frac{1}{2} + 3 + \frac{9}{2} = 3 + \frac{3 - 1 + 9}{2} = 3 + \frac{11}{2} = \frac{17}{2}\text{ sq . units }\]
\[ \therefore \text{Area of the bound region }= \frac{17}{2}\text{ sq . units }\]
APPEARS IN
RELATED QUESTIONS
Find the area of the region bounded by the parabola y2 = 4ax and its latus rectum.
Using integration, find the area bounded by the curve x2 = 4y and the line x = 4y − 2.
Area bounded by the curve y = x3, the x-axis and the ordinates x = –2 and x = 1 is ______.
Find the area of the region lying in the first quandrant bounded by the curve y2= 4x, X axis and the lines x = 1, x = 4
Find the area of the region bounded by the parabola y2 = 4ax and the line x = a.
Find the area lying above the x-axis and under the parabola y = 4x − x2.
Draw the rough sketch of y2 + 1 = x, x ≤ 2. Find the area enclosed by the curve and the line x = 2.
Using definite integrals, find the area of the circle x2 + y2 = a2.
Sketch the graph y = | x − 5 |. Evaluate \[\int\limits_0^1 \left| x - 5 \right| dx\]. What does this value of the integral represent on the graph.
Compare the areas under the curves y = cos2 x and y = sin2 x between x = 0 and x = π.
Find the area enclosed by the curve x = 3cost, y = 2sin t.
Find the area of the region bounded by x2 + 16y = 0 and its latusrectum.
Draw a rough sketch of the region {(x, y) : y2 ≤ 3x, 3x2 + 3y2 ≤ 16} and find the area enclosed by the region using method of integration.
The area bounded by y = 2 − x2 and x + y = 0 is _________ .
If An be the area bounded by the curve y = (tan x)n and the lines x = 0, y = 0 and x = π/4, then for x > 2
The area bounded by the parabola y2 = 4ax and x2 = 4ay is ___________ .
The area bounded by the curve y = x4 − 2x3 + x2 + 3 with x-axis and ordinates corresponding to the minima of y is _________ .
The closed area made by the parabola y = 2x2 and y = x2 + 4 is __________ .
The ratio of the areas between the curves y = cos x and y = cos 2x and x-axis from x = 0 to x = π/3 is ________ .
The area bounded by the parabola y2 = 8x, the x-axis and the latusrectum is ___________ .
Area of the region bounded by the curve y2 = 4x, y-axis and the line y = 3, is
Using integration, find the area of the region bounded by the line x – y + 2 = 0, the curve x = \[\sqrt{y}\] and y-axis.
Sketch the graphs of the curves y2 = x and y2 = 4 – 3x and find the area enclosed between them.
The area of the region bounded by the curve y = x2 and the line y = 16 ______.
Find the area of the region included between y2 = 9x and y = x
Find the area bounded by the curve y = `sqrt(x)`, x = 2y + 3 in the first quadrant and x-axis.
Draw a rough sketch of the given curve y = 1 + |x +1|, x = –3, x = 3, y = 0 and find the area of the region bounded by them, using integration.
The area of the region bounded by parabola y2 = x and the straight line 2y = x is ______.
Using integration, find the area of the region bounded between the line x = 4 and the parabola y2 = 16x.
Area lying in the first quadrant and bounded by the circle `x^2 + y^2 = 4` and the lines `x + 0` and `x = 2`.
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9` = 1.
Make a rough sketch of the region {(x, y): 0 ≤ y ≤ x2, 0 ≤ y ≤ x, 0 ≤ x ≤ 2} and find the area of the region using integration.
Find the area of the region bounded by curve 4x2 = y and the line y = 8x + 12, using integration.
The area of the region S = {(x, y): 3x2 ≤ 4y ≤ 6x + 24} is ______.
Area (in sq.units) of the region outside `|x|/2 + |y|/3` = 1 and inside the ellipse `x^2/4 + y^2/9` = 1 is ______.
Find the area of the following region using integration ((x, y) : y2 ≤ 2x and y ≥ x – 4).
Find the area of the region bounded by the curve x2 = 4y and the line x = 4y – 2.
Using integration, find the area of the region bounded by the curve y2 = 4x and x2 = 4y.
