Question

The area bounded by y = 2 − x² and x + y = 0 is _________ .

Options

• \[\frac{7}{2}\] sq. units

• \[\frac{9}{2}\] sq. units

• 9 sq. units

• none of these

Answer 1

\[\frac{9}{2}\text{ sq . units }\]

 

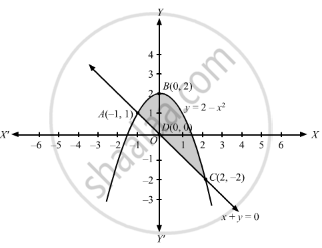
To find the points of intersection of x + y = 0 and y = 2 − x².
We put x = − y in y = 2 − x², we get \[y = 2 - y^2 \]
\[ \Rightarrow y^2 + y - 2 = 0\]
\[ \Rightarrow \left( y - 1 \right)\left( y + 2 \right) = 0\]
\[ \Rightarrow y = 1, - 2\]

\[\Rightarrow x = - 1, 2\]
Therefore, the points of intersection are A(−1, 1) and C(2, −2).
The area of the required region ABCD,
\[A = \int_{- 1}^2 \left( y_1 - y_2 \right) d x ...........\left(\text{Where, }y_1 = 2 - x^2\text{ and }y_2 = - x \right)\]
\[ = \int_{- 1}^2 \left( 2 - x^2 + x \right) d x\]
\[ = \left[ 2x - \frac{x^3}{3} + \frac{x^2}{2} \right]_{- 1}^2 \]
\[ = \left\{ 2\left( 2 \right) - \frac{\left( 2 \right)^3}{3} + \frac{\left( 2 \right)^2}{2} \right\} - \left\{ 2\left( - 1 \right) - \frac{\left( - 1 \right)^3}{3} + \frac{\left( - 1 \right)^2}{2} \right\}\]
\[ = \left( 4 - \frac{8}{3} + 2 \right) - \left( - 2 + \frac{1}{3} + \frac{1}{2} \right)\]
\[ = 6 - \frac{8}{3} + 2 - \frac{1}{3} - \frac{1}{2}\]
\[ = 8 - \frac{9}{3} - \frac{1}{2}\]
\[ = 5 - \frac{1}{2}\]
\[ = \frac{9}{2}\text{ square units }.\]