Advertisements
Advertisements
Question
Compute the area bounded by the lines x + 2y = 2, y – x = 1 and 2x + y = 7.
Solution
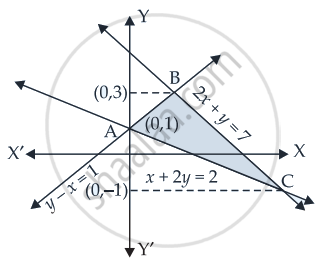
Given that: x + 2y = 2 .....(i)
y – x = 1 ......(ii)
And 2x + y = 7 ......(iii)
| x | 0 | 2 |
| y | 1 | 0 |
| x | 0 | –1 |
| y | 1 | 0 |
| x | 0 | `7/2` |
| y | 7 | 0 |
Solving equations (ii) and (iii)
We get y = 1 + x
∴ 2x + 1 + x = 7
3x = 6
⇒ x = 2
∴ y = 1 + 2
= 3
Coordinates of B = (2, 3)
Solving equations (i) and (iii)
We get x + 2y = 2
∴ x = 2 – 2y
2x + y = 7
2(2 – 2y) + y = 7
⇒ 4 – 4y + y = 7
⇒ –3y = 3
∴ y = –1 and x = 4
∴ Coordinates of C = (4, – 1) and coordinates of A = (0, 1).
Taking the limits on y-axis, we get
`int_(-1)^3 x_"BC" "d"y - int_(-1)^1 x_"AC" "d"y - int_1^3 x_"AB" "d"y`
= `int_(-1)^3 (7 - y)/2 "d"y - int_(-1)^1 (2 - 2y) "d"y - int_1^3 (y - 1) "d"y`
= `1/2 [7y - y^2/2]_-1^2 - 2[y - y^2/2]_-1^1 - [y^2/2 - y]_1^3`
= `1/2[(21 - 9/2) - (7 - 1/2)] - 2[(1 - 1/2) - (-1 - 1/2)] - [(9/2 - 3) - (1/2 - 1)]`
= `1/2[33/2 + 15/2] - 2[1/2 + 3/2] - [3/2 + 1/2]`
= `1/2 xx 24 - 2 xx 2 - 2`
⇒ 12 – 4 – 2 = 6 sq.units
Hence, the required area = 6 sq.units
APPEARS IN
RELATED QUESTIONS
Using the method of integration find the area of the region bounded by lines: 2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0
Find the area of ellipse `x^2/1 + y^2/4 = 1`
Find the area lying above the x-axis and under the parabola y = 4x − x2.
Sketch the graph y = | x + 1 |. Evaluate\[\int\limits_{- 4}^2 \left| x + 1 \right| dx\]. What does the value of this integral represent on the graph?
Draw a rough sketch of the curve \[y = \frac{x}{\pi} + 2 \sin^2 x\] and find the area between the x-axis, the curve and the ordinates x = 0 and x = π.
Find the area bounded by the ellipse \[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\] and the ordinates x = ae and x = 0, where b2 = a2 (1 − e2) and e < 1.
Find the area of the region bounded by the curve \[x = a t^2 , y = 2\text{ at }\]between the ordinates corresponding t = 1 and t = 2.
Calculate the area of the region bounded by the parabolas y2 = x and x2 = y.
Find the area of the region \[\left\{ \left( x, y \right): \frac{x^2}{a^2} + \frac{y^2}{b^2} \leq 1 \leq \frac{x}{a} + \frac{y}{b} \right\}\]
Using integration, find the area of the triangular region, the equations of whose sides are y = 2x + 1, y = 3x+ 1 and x = 4.
Draw a rough sketch of the region {(x, y) : y2 ≤ 5x, 5x2 + 5y2 ≤ 36} and find the area enclosed by the region using method of integration.
Prove that the area common to the two parabolas y = 2x2 and y = x2 + 4 is \[\frac{32}{3}\] sq. units.
Find the area of the region {(x, y): x2 + y2 ≤ 4, x + y ≥ 2}.
Using integration, find the area of the following region: \[\left\{ \left( x, y \right) : \frac{x^2}{9} + \frac{y^2}{4} \leq 1 \leq \frac{x}{3} + \frac{y}{2} \right\}\]
The area of the region formed by x2 + y2 − 6x − 4y + 12 ≤ 0, y ≤ x and x ≤ 5/2 is ______ .
Area bounded by parabola y2 = x and straight line 2y = x is _________ .
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices area A(1, 2), B (2, 0) and C (4, 3).
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using vertical strips.
Find the equation of the standard ellipse, taking its axes as the coordinate axes, whose minor axis is equal to the distance between the foci and whose length of the latus rectum is 10. Also, find its eccentricity.
Find the area of the region bound by the curves y = 6x – x2 and y = x2 – 2x
The area of the region bounded by the curve x = y2, y-axis and the line y = 3 and y = 4 is ______.
Find the area of the region bounded by the curves y2 = 9x, y = 3x
Sketch the region `{(x, 0) : y = sqrt(4 - x^2)}` and x-axis. Find the area of the region using integration.
Find the area enclosed by the curve y = –x2 and the straight lilne x + y + 2 = 0
Using integration, find the area of the region `{(x, y): 0 ≤ y ≤ sqrt(3)x, x^2 + y^2 ≤ 4}`
Area of the region bounded by the curve y = |x + 1| + 1, x = –3, x = 3 and y = 0 is
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9` = 1.
Let g(x) = cosx2, f(x) = `sqrt(x)`, and α, β (α < β) be the roots of the quadratic equation 18x2 – 9πx + π2 = 0. Then the area (in sq. units) bounded by the curve y = (gof)(x) and the lines x = α, x = β and y = 0, is ______.
Sketch the region bounded by the lines 2x + y = 8, y = 2, y = 4 and the Y-axis. Hence, obtain its area using integration.
