Question

Find the area of the region bounded by the curve \[x = a t^2 , y = 2\text{ at }\]between the ordinates corresponding t = 1 and t = 2.

Answer 1

The curve \[x = a t^2 , y = 2\text{ at }\]  represents the parametric equation of the parabola.

Eliminating the parameter t, we get \[y^2 = 4ax\]

This represents the Cartesian equation of the parabola opening towards the positive x-axis with focus at (a, 0).

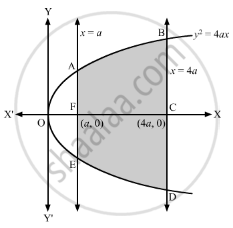
When t = 1, x = a

When t = 2, x = 4a

∴ Required area = Area of the shaded region
                           = 2 × Area of the region ABCFA

\[= 2 \int_a^{4a} y_{\text{ parabola }} dx\]
\[ = 2 \int_a^{4a} \sqrt{4ax}dx\]
\[ = \left.2 \times {2\sqrt{a} \times \frac{x^\frac{3}{2}}{\frac{3}{2}}}\right|_a^{4a} \]
\[ = \frac{8\sqrt{a}}{3}\left[ \left( 4a \right)^\frac{3}{2} - a^\frac{3}{2} \right]\]
\[ = \frac{8\sqrt{a}}{3}\left( 8a\sqrt{a} - a\sqrt{a} \right)\]
\[ = \frac{8\sqrt{a}}{3} \times 7a\sqrt{a}\]
\[ = \frac{56}{3} a^2\text{ square units }\]