Advertisements
Advertisements
Question
Find the area of the region bound by the curves y = 6x – x2 and y = x2 – 2x
Solution
y = 6x - x2, y = x2 - 2x
x2 - 6x = - y
⇒ x2 - 6x + 9 = - y + 9
⇒ ( x - 3 )2 = - ( y - 9 )
This represents a downward parabola with vertex (3, 9) ...(i)
y = x2 - 2x
x2 - 2x + 1 = y + 1
⇒ ( x - 1 )2 = y + 1
⇒ ( x -1 )2 = y - ( -1 ) ...(ii)
This represents an upward parabola with vertex (1, -1)
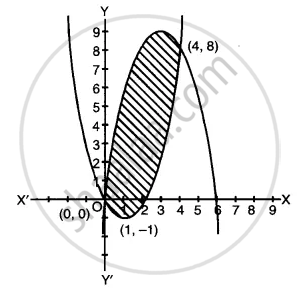
Point of intersection is given by:
6x - x2 = x2 - 2x
⇒ 2x2 = 8x
⇒ x2 - 4x = 0
⇒ x (x - 4) = 0
x = 0, x = 4
y = 6 x 4 - 42
= 24 - 16 = 8
Point of intersection is (0, 0) ; (4, 8)
Reqd. area = ` int_0^4 (6x - x^2) - (x^2 - 2x) dx`
= `int_0^4 8x - 2x^2 dx = [ (8x^2)/(2) - (2)/(3) x^3]_0^4`
= 4 x 42 - `(2)/(3) (4)^3 = (64)/(3)` sq. units.
APPEARS IN
RELATED QUESTIONS
Find the area bounded by the curve y2 = 4ax, x-axis and the lines x = 0 and x = a.
Sketch the graph of y = |x + 4|. Using integration, find the area of the region bounded by the curve y = |x + 4| and x = –6 and x = 0.
Draw a rough sketch to indicate the region bounded between the curve y2 = 4x and the line x = 3. Also, find the area of this region.
Draw a rough sketch of the graph of the function y = 2 \[\sqrt{1 - x^2}\] , x ∈ [0, 1] and evaluate the area enclosed between the curve and the x-axis.
Show that the areas under the curves y = sin x and y = sin 2x between x = 0 and x =\[\frac{\pi}{3}\] are in the ratio 2 : 3.
Compare the areas under the curves y = cos2 x and y = sin2 x between x = 0 and x = π.
Find the area enclosed by the curve x = 3cost, y = 2sin t.
Find the area of the region in the first quadrant bounded by the parabola y = 4x2 and the lines x = 0, y = 1 and y = 4.
Draw a rough sketch of the region {(x, y) : y2 ≤ 5x, 5x2 + 5y2 ≤ 36} and find the area enclosed by the region using method of integration.
Find the area enclosed by the parabolas y = 5x2 and y = 2x2 + 9.
Find the area of the region in the first quadrant enclosed by x-axis, the line y = \[\sqrt{3}x\] and the circle x2 + y2 = 16.
If the area above the x-axis, bounded by the curves y = 2kx and x = 0, and x = 2 is \[\frac{3}{\log_e 2}\], then the value of k is __________ .
If An be the area bounded by the curve y = (tan x)n and the lines x = 0, y = 0 and x = π/4, then for x > 2
Area bounded by the curve y = x3, the x-axis and the ordinates x = −2 and x = 1 is ______.
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
Find the area of the region bounded by the parabolas y2 = 6x and x2 = 6y.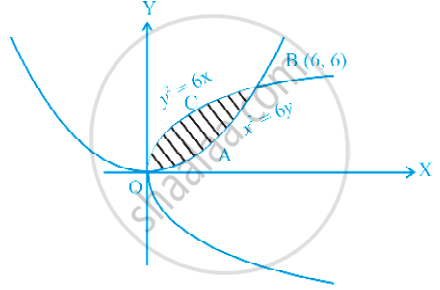
Find the area of the region included between y2 = 9x and y = x
Find the area bounded by the curve y = `sqrt(x)`, x = 2y + 3 in the first quadrant and x-axis.
Draw a rough sketch of the region {(x, y) : y2 ≤ 6ax and x 2 + y2 ≤ 16a2}. Also find the area of the region sketched using method of integration.
Find the area bounded by the lines y = 4x + 5, y = 5 – x and 4y = x + 5.
The area of the region bounded by the curve y = sinx between the ordinates x = 0, x = `pi/2` and the x-axis is ______.
The area of the region bounded by the circle x2 + y2 = 1 is ______.
The area of the region bounded by the line y = 4 and the curve y = x2 is ______.
The area bounded by `y`-axis, `y = cosx` and `y = sinx, 0 ≤ x - (<pi)/2` is
Find the area bounded by the curve y = |x – 1| and y = 1, using integration.
Let the curve y = y(x) be the solution of the differential equation, `("dy")/("d"x) = 2(x + 1)`. If the numerical value of area bounded by the curve y = y(x) and x-axis is `(4sqrt(8))/3`, then the value of y(1) is equal to ______.
Let P(x) be a real polynomial of degree 3 which vanishes at x = –3. Let P(x) have local minima at x = 1, local maxima at x = –1 and `int_-1^1 P(x)dx` = 18, then the sum of all the coefficients of the polynomial P(x) is equal to ______.
Using integration, find the area of the region bounded by y = mx (m > 0), x = 1, x = 2 and the X-axis.
Find the area of the region bounded by the curve x2 = 4y and the line x = 4y – 2.
Sketch the region enclosed bounded by the curve, y = x |x| and the ordinates x = −1 and x = 1.
