Advertisements
Advertisements
Question
The area of the region bounded by the curve y = sinx between the ordinates x = 0, x = `pi/2` and the x-axis is ______.
Options
2 sq.units
4 sq.units
3 sq.units
1 sq.unit
Solution
The area of the region bounded by the curve y = sinx between the ordinates x = 0, x = `pi/2` and the x-axis is 1 sq.unit.
Explanation: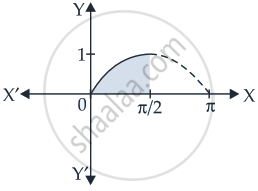
= `int_0^(pi/2) sin x "d"x`
= `- [cos x]_0^(pi/2)`
= `-[cos pi/2 - cos 0]`
= `-[0 - 1]`
= 1 sq.unit
APPEARS IN
RELATED QUESTIONS
Find the area of the region bounded by the parabola y2 = 4ax and its latus rectum.
Find the area of the sector of a circle bounded by the circle x2 + y2 = 16 and the line y = x in the ftrst quadrant.
Find the area of the region bounded by the curve x2 = 16y, lines y = 2, y = 6 and Y-axis lying in the first quadrant.
Find the equation of a curve passing through the point (0, 2), given that the sum of the coordinates of any point on the curve exceeds the slope of the tangent to the curve at that point by 5.
Sketch the graph y = | x + 3 |. Evaluate \[\int\limits_{- 6}^0 \left| x + 3 \right| dx\]. What does this integral represent on the graph?
Find the area of the region common to the parabolas 4y2 = 9x and 3x2 = 16y.
Find the area enclosed by the curve \[y = - x^2\] and the straight line x + y + 2 = 0.
Using the method of integration, find the area of the region bounded by the following lines:
3x − y − 3 = 0, 2x + y − 12 = 0, x − 2y − 1 = 0.
Sketch the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 1. Also, find the area of this region.
Using integration, find the area of the triangle ABC coordinates of whose vertices are A (4, 1), B (6, 6) and C (8, 4).
Find the area of the circle x2 + y2 = 16 which is exterior to the parabola y2 = 6x.
Make a sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 3; 0 ≤ y ≤ 2x + 3; 0 ≤ x ≤ 3} and find its area using integration.
Find the area of the region bounded by the curve y = \[\sqrt{1 - x^2}\], line y = x and the positive x-axis.
Find the area of the region {(x, y): x2 + y2 ≤ 4, x + y ≥ 2}.
Find the area of the region bounded by the parabola y2 = 2x and the straight line x − y = 4.
If the area above the x-axis, bounded by the curves y = 2kx and x = 0, and x = 2 is \[\frac{3}{\log_e 2}\], then the value of k is __________ .
If An be the area bounded by the curve y = (tan x)n and the lines x = 0, y = 0 and x = π/4, then for x > 2
The area bounded by the parabola y2 = 4ax, latusrectum and x-axis is ___________ .
Area bounded by the curve y = x3, the x-axis and the ordinates x = −2 and x = 1 is ______.
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
Using integration, find the area of the smaller region bounded by the ellipse `"x"^2/9+"y"^2/4=1`and the line `"x"/3+"y"/2=1.`
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2
The area of the region bounded by the curve y = x + 1 and the lines x = 2 and x = 3 is ______.
Area of the region bounded by the curve y = |x + 1| + 1, x = –3, x = 3 and y = 0 is
The area of the region S = {(x, y): 3x2 ≤ 4y ≤ 6x + 24} is ______.
Area (in sq.units) of the region outside `|x|/2 + |y|/3` = 1 and inside the ellipse `x^2/4 + y^2/9` = 1 is ______.
Sketch the region bounded by the lines 2x + y = 8, y = 2, y = 4 and the Y-axis. Hence, obtain its area using integration.
Evaluate:
`int_0^1x^2dx`
