Advertisements
Advertisements
Question
Make a sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 3; 0 ≤ y ≤ 2x + 3; 0 ≤ x ≤ 3} and find its area using integration.
Solution

\[R = \left\{ \left( x, y \right): 0 \leq y \leq x^2 + 3 , 0 \leq y \leq 2x + 3 , 0 \leq x \leq 3 \right\}\]
\[ R_1 = \left\{ \left( x, y \right) : 0 \leq y \leq x^2 + 3 \right\}\]
\[ R_2 = \left\{ \left( x, y \right) : 0 \leq y \leq 2x + 3 \right\}\]
\[ R_3 = \left\{ \left( x, y \right) : 0 \leq x \leq 3 \right\}\]
\[ \Rightarrow R = R_1 \cap R_2 \cap R_3 \]
y = x2 + 3 is a upward opening parabola with vertex A(0, 3).
Thus R1 is the region above x-axis and below the parabola
y = 2x + 3 is a straight line passing through A(0, 3) and cuts y-axis on (−3/2, 0).
Hence R2 is the region above x-axis and below the line
x = 3 is a straight line parallel to y-axis, cutting x-axis at E(3, 0).
Hence R3 is the region above x-axis and to the left of the line x = 3.
Point of intersection of the parabola and y = 2x + 3 is given by solving the two equations
\[y = x^2 + 3\]
\[y = 2x + 3\]
\[ \Rightarrow x^2 + 3 = 2x + 3\]
\[ \Rightarrow x^2 - 2x = 0\]
\[ \Rightarrow x\left( x - 2 \right) = 0\]
\[ \Rightarrow x = 0 \text{ or }x = 2\]
\[ \Rightarrow y = 3\text{ or }y = 7\]
\[ \Rightarrow A\left( 0, 3 \right)\text{ and }B\left( 2, 7 \right) \text{ are points of intersection }\]
\[\text{ Also }, x = 3\text{ cuts the parabola at }C\left( 3, 12 \right)\]
\[\text{ and }x = 3\text{ cuts }y = 2x + 3\text{ at }D\left( 3, 9 \right)\]
We require thearea of shaded region.
\[\text{ Total shaded area }= \int_0^2 \left( x^2 + 3 \right)dx + \int_2^3 \left( 2x + 3 \right)dx\]
\[ = \left[ \frac{x^3}{3} + 3x \right]_0^2 + \left[ \frac{2 x^2}{2} + 3x \right]_2^3 \]
\[ = \left[ \frac{x^3}{3} + 3x \right]_0^2 + \left[ x^2 + 3x \right]_2^3 \]
\[ = \left[ \frac{8}{3} + 6 \right] + \left[ 9 + 9 - 4 - 6 \right]\]
\[ = \frac{8}{3} + 6 + 8\]
\[ = \frac{8 + 42}{3}\]
\[ = \frac{50}{3}\text{ sq . units }\]
APPEARS IN
RELATED QUESTIONS
Find the area bounded by the curve y = sin x between x = 0 and x = 2π.
Make a rough sketch of the graph of the function y = 4 − x2, 0 ≤ x ≤ 2 and determine the area enclosed by the curve, the x-axis and the lines x = 0 and x = 2.
Using integration, find the area of the region bounded by the line 2y = 5x + 7, x-axis and the lines x = 2 and x = 8.
Using definite integrals, find the area of the circle x2 + y2 = a2.
Find the area of the minor segment of the circle \[x^2 + y^2 = a^2\] cut off by the line \[x = \frac{a}{2}\]
Find the area of the region bounded by the curve \[a y^2 = x^3\], the y-axis and the lines y = a and y = 2a.
Using integration, find the area of the region bounded by the triangle whose vertices are (2, 1), (3, 4) and (5, 2).
Using integration, find the area of the region bounded by the triangle ABC whose vertices A, B, C are (−1, 1), (0, 5) and (3, 2) respectively.
Find the area of the region between the circles x2 + y2 = 4 and (x − 2)2 + y2 = 4.
Draw a rough sketch of the region {(x, y) : y2 ≤ 3x, 3x2 + 3y2 ≤ 16} and find the area enclosed by the region using method of integration.
Using integration, find the area of the region bounded by the triangle whose vertices are (−1, 2), (1, 5) and (3, 4).
Find the area of the region in the first quadrant enclosed by x-axis, the line y = \[\sqrt{3}x\] and the circle x2 + y2 = 16.
Find the area of the region bounded by the curves y = x − 1 and (y − 1)2 = 4 (x + 1).
Find the area of the region bounded by y = | x − 1 | and y = 1.
Using integration, find the area of the following region: \[\left\{ \left( x, y \right) : \frac{x^2}{9} + \frac{y^2}{4} \leq 1 \leq \frac{x}{3} + \frac{y}{2} \right\}\]
If the area bounded by the parabola \[y^2 = 4ax\] and the line y = mx is \[\frac{a^2}{12}\] sq. units, then using integration, find the value of m.
The area included between the parabolas y2 = 4x and x2 = 4y is (in square units)
The area bounded by the parabola y2 = 4ax and x2 = 4ay is ___________ .
The closed area made by the parabola y = 2x2 and y = x2 + 4 is __________ .
Area lying in first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2, is
Find the equation of the parabola with latus-rectum joining points (4, 6) and (4, -2).
Find the area of the region bound by the curves y = 6x – x2 and y = x2 – 2x
Find the area of the region bounded by the parabolas y2 = 6x and x2 = 6y.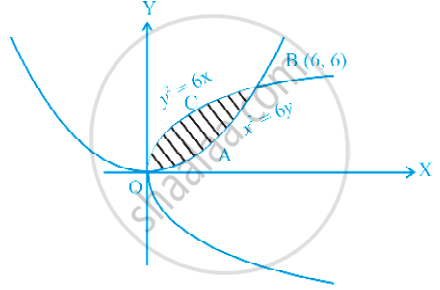
The area of the region bounded by the curve x = y2, y-axis and the line y = 3 and y = 4 is ______.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2
Using integration, find the area of the region bounded by the line 2y = 5x + 7, x- axis and the lines x = 2 and x = 8.
Find the area of the region bounded by the curve y2 = 2x and x2 + y2 = 4x.
Compute the area bounded by the lines x + 2y = 2, y – x = 1 and 2x + y = 7.
Find the area bounded by the curve y = 2cosx and the x-axis from x = 0 to x = 2π
Area of the region bounded by the curve y = cosx between x = 0 and x = π is ______.
The region bounded by the curves `x = 1/2, x = 2, y = log x` and `y = 2^x`, then the area of this region, is
Find the area of the region bounded by the curve `y = x^2 + 2, y = x, x = 0` and `x = 3`
The area bounded by the curve `y = x|x|`, `x`-axis and the ordinate `x` = – 1 and `x` = 1 is given by
Make a rough sketch of the region {(x, y): 0 ≤ y ≤ x2, 0 ≤ y ≤ x, 0 ≤ x ≤ 2} and find the area of the region using integration.
Area of figure bounded by straight lines x = 0, x = 2 and the curves y = 2x, y = 2x – x2 is ______.
The area of the region bounded by the parabola (y – 2)2 = (x – 1), the tangent to it at the point whose ordinate is 3 and the x-axis is ______.
