Advertisements
Advertisements
Question
Using integration, find the area of the region bounded by the line 2y = 5x + 7, x-axis and the lines x = 2 and x = 8.
Solution
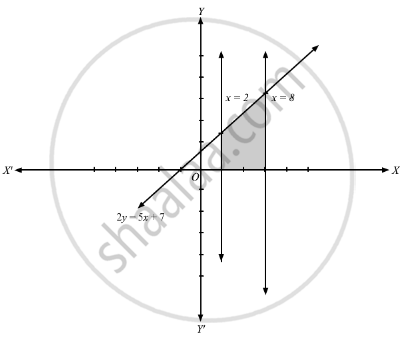
We have,
Straight line 2y = 5x + 7 intersect x-axis and y-axis at ( −1.4, 0) and (0, 3.5) respectively.
Also x = 2 and x = 8 are straight lines as shown in the figure.
The shaded region is our required region whose area has to be found.
When we slice the shaded region into vertical strips, we find that each vertical strip has its lower end on x-axis and upper end on the line
2y = 5x + 7
So, approximating rectangle shown in figure has length = y and width = dx and area = y dx.
The approximating rectangle can move from x = 2 to x = 8.
So, required is given by,
\[A = \int_2^8 y d x\]
\[ = \int_2^8 \left( \frac{5x + 7}{2} \right) d x\]
\[ = \frac{1}{2} \int_2^8 (5x + 7) dx\]
\[ = \frac{1}{2} \left[ \frac{5}{2} x^2 + 7x \right]_2^8 \]
\[ = \frac{1}{2}\left[ \frac{5}{2} \times 64 + 56 - \frac{5}{2} \times 4 - 14 \right]\]
\[ = \frac{1}{2} \times 192\]
\[ = 96\text{ sq units }\]
APPEARS IN
RELATED QUESTIONS
The area bounded by the curve y = x | x|, x-axis and the ordinates x = –1 and x = 1 is given by ______.
[Hint: y = x2 if x > 0 and y = –x2 if x < 0]
Find the equation of a curve passing through the point (0, 2), given that the sum of the coordinates of any point on the curve exceeds the slope of the tangent to the curve at that point by 5
Find the area lying above the x-axis and under the parabola y = 4x − x2.
Draw a rough sketch of the graph of the function y = 2 \[\sqrt{1 - x^2}\] , x ∈ [0, 1] and evaluate the area enclosed between the curve and the x-axis.
Draw a rough sketch of the curve y = \[\frac{\pi}{2} + 2 \sin^2 x\] and find the area between x-axis, the curve and the ordinates x = 0, x = π.
Find the area of the region in the first quadrant bounded by the parabola y = 4x2 and the lines x = 0, y = 1 and y = 4.
Find the area of the region bounded by x2 = 16y, y = 1, y = 4 and the y-axis in the first quadrant.
Find the area of the region bounded by x2 + 16y = 0 and its latusrectum.
Using integration, find the area of the region bounded by the triangle whose vertices are (−1, 2), (1, 5) and (3, 4).
Find the area of the region bounded by the curves y = x − 1 and (y − 1)2 = 4 (x + 1).
Using integration, find the area of the triangle ABC coordinates of whose vertices are A (4, 1), B (6, 6) and C (8, 4).
Using integration find the area of the region:
\[\left\{ \left( x, y \right) : \left| x - 1 \right| \leq y \leq \sqrt{5 - x^2} \right\}\]
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2.
If the area enclosed by the parabolas y2 = 16ax and x2 = 16ay, a > 0 is \[\frac{1024}{3}\] square units, find the value of a.
The closed area made by the parabola y = 2x2 and y = x2 + 4 is __________ .
The ratio of the areas between the curves y = cos x and y = cos 2x and x-axis from x = 0 to x = π/3 is ________ .
The area bounded by the parabola y2 = 8x, the x-axis and the latusrectum is ___________ .
Area bounded by the curve y = x3, the x-axis and the ordinates x = −2 and x = 1 is ______.
The area bounded by the curve y = x |x| and the ordinates x = −1 and x = 1 is given by
The area bounded by the y-axis, y = cos x and y = sin x when 0 ≤ x ≤ \[\frac{\pi}{2}\] is _________ .
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using vertical strips.
Find the equation of the standard ellipse, taking its axes as the coordinate axes, whose minor axis is equal to the distance between the foci and whose length of the latus rectum is 10. Also, find its eccentricity.
The area of the region bounded by the curve y = x2 and the line y = 16 ______.
Find the area bounded by the curve y = sinx between x = 0 and x = 2π.
Draw a rough sketch of the given curve y = 1 + |x +1|, x = –3, x = 3, y = 0 and find the area of the region bounded by them, using integration.
The area of the region bounded by the curve x2 = 4y and the straight line x = 4y – 2 is ______.
The area of the region bounded by the curve y = x + 1 and the lines x = 2 and x = 3 is ______.
Using integration, find the area of the region `{(x, y): 0 ≤ y ≤ sqrt(3)x, x^2 + y^2 ≤ 4}`
Area of the region bounded by the curve `y^2 = 4x`, `y`-axis and the line `y` = 3 is:
Make a rough sketch of the region {(x, y): 0 ≤ y ≤ x2, 0 ≤ y ≤ x, 0 ≤ x ≤ 2} and find the area of the region using integration.
Find the area of the region bounded by curve 4x2 = y and the line y = 8x + 12, using integration.
Let T be the tangent to the ellipse E: x2 + 4y2 = 5 at the point P(1, 1). If the area of the region bounded by the tangent T, ellipse E, lines x = 1 and x = `sqrt(5)` is `sqrt(5)`α + β + γ `cos^-1(1/sqrt(5))`, then |α + β + γ| is equal to ______.
The area of the region S = {(x, y): 3x2 ≤ 4y ≤ 6x + 24} is ______.
The area of the region bounded by the parabola (y – 2)2 = (x – 1), the tangent to it at the point whose ordinate is 3 and the x-axis is ______.
The area (in square units) of the region bounded by the curves y + 2x2 = 0 and y + 3x2 = 1, is equal to ______.
Using integration, find the area of the region bounded by line y = `sqrt(3)x`, the curve y = `sqrt(4 - x^2)` and Y-axis in first quadrant.
Using integration, find the area of the region bounded by the curve y2 = 4x and x2 = 4y.
