Advertisements
Advertisements
Question
Find the area of the region common to the parabolas 4y2 = 9x and 3x2 = 16y.
Solution
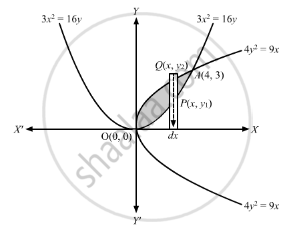
\[3 x^2 = 16 y . . . \left( 1 \right)\text{ is a parabola with vertex at (0, 0) opening upwards and symmetrical about + ve }y -\text{ axis }\]
\[4 y^2 = 9x . . . \left( 2 \right)\text{ is a parabola with vertex at (0, 0) opening sideways and symmetrical about + ve }x -\text{ axis }\]
\[\text{ Solving the equations }\left( 1 \right)\text{ and }\left( 2 \right), \text{ we get the points of intersection of the two parabolas O(0, 0) and A(4, 3 ) }\]
\[\text{ Consider a vertical strip of length }= \left| y_2 - y_1 \right|\text{ and width }= dx\text{ such that }P(x, y_1 )\text{ lies on }\left( 1 \right)\text{ and }Q(x, y_2 )\text{ lies on }\left( 2 \right)\]
\[ \Rightarrow\text{ area of approximating rectangle }= \left| y_2 - y_1 \right| dx\]
\[ \text{ Approximating rectangle moves from }x = 0\text{ to }x = 4\]
\[ \Rightarrow\text{ Area of the shaded region }= \int_0^4 \left| y_2 - y_1 \right| dx = \int_0^4 \left( y_2 - y_1 \right) dx ..................\left[\text{ As, }\left| y_2 - y_1 \right| = y_2 - y_1\text{ for }y_2 - y_1 > 0 \right] \]
\[ \Rightarrow A = \int_0^4 \left( \sqrt{\frac{9}{4}x} - \frac{3}{16} x^2 \right) dx \]
\[ \Rightarrow A = \frac{3}{2} \int_0^4 \sqrt{x} dx - \frac{3}{16} \int_0^4 x^2 dx \]
\[ \Rightarrow A = \frac{3}{2} \left[ \frac{x^\frac{3}{2}}{\frac{3}{2}} \right]_0^4 - \frac{3}{16} \left[ \frac{x^3}{3} \right]_0^4 \]
\[ \Rightarrow A = 4^\frac{3}{2} - \left( \frac{1}{16} \times 4^3 \right)\]
\[ \Rightarrow A = 8 - 4 = 4 \text{ sq . units }\]
\[ \therefore \text{ Area bound by the two curves = 4 sq . units }\]
APPEARS IN
RELATED QUESTIONS
Find the area of the region bounded by the parabola y2 = 4ax and its latus rectum.
Find the area of the region bounded by the parabola y2 = 16x and the line x = 3.
Find the area of the sector of a circle bounded by the circle x2 + y2 = 16 and the line y = x in the ftrst quadrant.
Find the area of ellipse `x^2/1 + y^2/4 = 1`
Using integration, find the area of the region bounded by the line y − 1 = x, the x − axis and the ordinates x= −2 and x = 3.
Using integration, find the area of the region bounded by the line 2y = 5x + 7, x-axis and the lines x = 2 and x = 8.
Using definite integrals, find the area of the circle x2 + y2 = a2.
Find the area of the region bounded by the curve xy − 3x − 2y − 10 = 0, x-axis and the lines x = 3, x = 4.
Find the area of the region bounded by the curve \[x = a t^2 , y = 2\text{ at }\]between the ordinates corresponding t = 1 and t = 2.
Find the area of the region in the first quadrant bounded by the parabola y = 4x2 and the lines x = 0, y = 1 and y = 4.
Find the area of the region bounded by the curve \[a y^2 = x^3\], the y-axis and the lines y = a and y = 2a.
Calculate the area of the region bounded by the parabolas y2 = x and x2 = y.
Using integration, find the area of the triangular region, the equations of whose sides are y = 2x + 1, y = 3x+ 1 and x = 4.
Draw a rough sketch of the region {(x, y) : y2 ≤ 3x, 3x2 + 3y2 ≤ 16} and find the area enclosed by the region using method of integration.
Find the area of the region in the first quadrant enclosed by x-axis, the line y = \[\sqrt{3}x\] and the circle x2 + y2 = 16.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2.
Find the area of the region {(x, y): x2 + y2 ≤ 4, x + y ≥ 2}.
The area bounded by the curve y = loge x and x-axis and the straight line x = e is ___________ .
The area bounded by the curves y = sin x between the ordinates x = 0, x = π and the x-axis is _____________ .
The ratio of the areas between the curves y = cos x and y = cos 2x and x-axis from x = 0 to x = π/3 is ________ .
Area bounded by parabola y2 = x and straight line 2y = x is _________ .
The area of the circle x2 + y2 = 16 enterior to the parabola y2 = 6x is
Sketch the graphs of the curves y2 = x and y2 = 4 – 3x and find the area enclosed between them.
Using integration, find the area of the smaller region bounded by the ellipse `"x"^2/9+"y"^2/4=1`and the line `"x"/3+"y"/2=1.`
Find the area of the region bounded by the curve ay2 = x3, the y-axis and the lines y = a and y = 2a.
Find the area of region bounded by the line x = 2 and the parabola y2 = 8x
Find the area of the region bounded by the curve y2 = 2x and x2 + y2 = 4x.
Find the area bounded by the curve y = sinx between x = 0 and x = 2π.
Using integration, find the area of the region bounded between the line x = 4 and the parabola y2 = 16x.
The area of the region enclosed by the parabola x2 = y, the line y = x + 2 and the x-axis, is
The region bounded by the curves `x = 1/2, x = 2, y = log x` and `y = 2^x`, then the area of this region, is
Find the area of the region bounded by `y^2 = 9x, x = 2, x = 4` and the `x`-axis in the first quadrant.
What is the area of the region bounded by the curve `y^2 = 4x` and the line `x` = 3.
The area bounded by the curve `y = x^3`, the `x`-axis and ordinates `x` = – 2 and `x` = 1
Find the area of the region bounded by curve 4x2 = y and the line y = 8x + 12, using integration.
Area (in sq.units) of the region outside `|x|/2 + |y|/3` = 1 and inside the ellipse `x^2/4 + y^2/9` = 1 is ______.
The area (in sq.units) of the region A = {(x, y) ∈ R × R/0 ≤ x ≤ 3, 0 ≤ y ≤ 4, y ≤x2 + 3x} is ______.
Let a and b respectively be the points of local maximum and local minimum of the function f(x) = 2x3 – 3x2 – 12x. If A is the total area of the region bounded by y = f(x), the x-axis and the lines x = a and x = b, then 4A is equal to ______.
Let P(x) be a real polynomial of degree 3 which vanishes at x = –3. Let P(x) have local minima at x = 1, local maxima at x = –1 and `int_-1^1 P(x)dx` = 18, then the sum of all the coefficients of the polynomial P(x) is equal to ______.
Evaluate:
`int_0^1x^2dx`
