Advertisements
Advertisements
Question
The area of the circle x2 + y2 = 16 enterior to the parabola y2 = 6x is
Options
- \[\frac{4}{3}\left( 4\pi - \sqrt{3} \right)\]
- \[\frac{4}{3}\left( 4\pi + \sqrt{3} \right)\]
- \[\frac{4}{3}\left( 8\pi - \sqrt{3} \right)\]
- \[\frac{4}{3}\left( 8\pi + \sqrt{3} \right)\]
Solution

Points of intersection of the parabola and the circle is obtained by solving the simultaneous equations
\[x^2 + y^2 = 16\text{ and }y^2 = 6x\]
\[ \Rightarrow x^2 + 6x = 16 \]
\[ \Rightarrow x^2 + 6x - 16 = 0\]
\[ \Rightarrow \left( x + 8 \right)\left( x - 2 \right) = 0\]
\[ \Rightarrow x = 2\text{ or }x = - 8 \]
\[x\text{ can not be - 8 as in this case it will be the point outside circle . }\]
\[ \therefore x = 2\]
\[ \therefore\text{ When }x = 2, y = \pm \sqrt{6 \times 2} = \pm \sqrt{12} = \pm 2\sqrt{3}\]
\[ \therefore B\left( 2 , 2\sqrt{3} \right)\text{ and }B'\left( 2 , - 2\sqrt{3} \right)\text{ are points of intersection of the parabola and circle . }\]
\[\text{ Required area = Area }\left( OB'C'A'CBO \right) =\text{ area of circle - area }\left( OBAB'O \right) \]
\[\text{ Area of circle with radius }4 = \pi \times 4^2 = 16\pi \]
Now,
\[\text{ Area }\left( OBAB'O \right) = 2\text{ area }\left( OBAO \right)\]
\[ = 2\left[\text{ area }\left( OBDO \right) +\text{ area }\left( DBAD \right) \right]\]
\[ = 2 \times \left[ \int_0^2 \sqrt{6x} dx + \int_2^4 \sqrt{16 - x^2} dx \right]\]
\[ = 2 \times \left\{ \left[ \sqrt{6}\frac{x^\frac{3}{2}}{\frac{3}{2}} \right]_0^2 + \left[ \frac{x}{2}\sqrt{16 - x^2} + \frac{1}{2} \times 16 \sin^{- 1} \left( \frac{x}{4} \right) \right]_2^4 \right\}\]
\[ = 2 \times \left\{ \left( \sqrt{6} \times \frac{2}{3} \times 2^\frac{3}{2} - 0 \right) + \left( \frac{1}{2}4\sqrt{16 - \left( 4 \right)^2} + \frac{1}{2} \times 16 \sin^{- 1} \frac{4}{4} - \frac{2}{2}\sqrt{16 - 2^2} - \frac{1}{2} \times 16 \sin^{- 1} \frac{2}{4} \right) \right\}\]
\[ = 2 \times \left[ \left( \sqrt{6} \times \frac{2}{3} \times 2\sqrt{2} \right) + 0 + 8 \sin^{- 1} \left( 1 \right) - \sqrt{12} - 8 \sin^{- 1} \left( \frac{1}{2} \right) \right]\]
\[ = 2 \times \left[ \frac{8\sqrt{3}}{3} + 8 \times \frac{\pi}{2} - 2\sqrt{3} - 8\frac{\pi}{6} \right]\]
\[ = 2 \left\{ \frac{8\sqrt{3} - 6\sqrt{3}}{3} + 8\left( \frac{\pi}{2} - \frac{\pi}{6} \right) \right\}\]
\[ = 2\left\{ \frac{2\sqrt{3}}{3} + 8\left( \frac{2\pi}{6} \right) \right\}\]
\[ = \frac{4\sqrt{3}}{3} + \frac{16\pi}{3}\]
\[\text{ Shaded area }= 16\pi - \left( \frac{4\sqrt{3}}{3} + \frac{16\pi}{3} \right)\]
\[ = \frac{48\pi - 16\pi}{3} - \frac{4\sqrt{3}}{3}\]
\[ = \frac{32\pi}{3} - \frac{4\sqrt{3}}{3}\]
\[ = \frac{4}{3}\left( 8\pi - \sqrt{3} \right)\text{ sq units }\]
APPEARS IN
RELATED QUESTIONS
Find the area of the region common to the circle x2 + y2 =9 and the parabola y2 =8x
Using integration, find the area of the region bounded by the lines y = 2 + x, y = 2 – x and x = 2.
Using integration, find the area of the region bounded between the line x = 2 and the parabola y2 = 8x.
Using integration, find the area of the region bounded by the line y − 1 = x, the x − axis and the ordinates x= −2 and x = 3.
Find the area lying above the x-axis and under the parabola y = 4x − x2.
Find the area of the minor segment of the circle \[x^2 + y^2 = a^2\] cut off by the line \[x = \frac{a}{2}\]
Find the area enclosed by the curve x = 3cost, y = 2sin t.
Using integration, find the area of the region bounded by the triangle whose vertices are (2, 1), (3, 4) and (5, 2).
Using integration, find the area of the triangular region, the equations of whose sides are y = 2x + 1, y = 3x+ 1 and x = 4.
Find the area of the region common to the circle x2 + y2 = 16 and the parabola y2 = 6x.
Prove that the area common to the two parabolas y = 2x2 and y = x2 + 4 is \[\frac{32}{3}\] sq. units.
Find the area bounded by the parabola y = 2 − x2 and the straight line y + x = 0.
Using integration find the area of the region:
\[\left\{ \left( x, y \right) : \left| x - 1 \right| \leq y \leq \sqrt{5 - x^2} \right\}\]
Find the area bounded by the lines y = 4x + 5, y = 5 − x and 4y = x + 5.
Find the area of the figure bounded by the curves y = | x − 1 | and y = 3 −| x |.
Find the area of the region between the parabola x = 4y − y2 and the line x = 2y − 3.
The area of the region formed by x2 + y2 − 6x − 4y + 12 ≤ 0, y ≤ x and x ≤ 5/2 is ______ .
The area bounded by the curve y = 4x − x2 and the x-axis is __________ .
The area bounded by the curve y = x |x| and the ordinates x = −1 and x = 1 is given by
Sketch the graphs of the curves y2 = x and y2 = 4 – 3x and find the area enclosed between them.
Using the method of integration, find the area of the region bounded by the lines 3x − 2y + 1 = 0, 2x + 3y − 21 = 0 and x − 5y + 9 = 0
Find the area of the region bounded by the parabola y2 = 2x and the straight line x – y = 4.
Find the area of the region bounded by the parabolas y2 = 6x and x2 = 6y.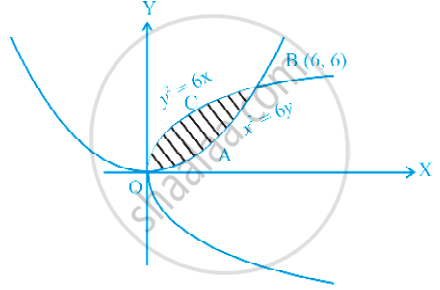
The area of the region bounded by the curve x = y2, y-axis and the line y = 3 and y = 4 is ______.
Find the area of the region bounded by the curves y2 = 9x, y = 3x
Find the area of the region included between y2 = 9x and y = x
Find the area of the region bounded by y = `sqrt(x)` and y = x.
Find the area bounded by the curve y = `sqrt(x)`, x = 2y + 3 in the first quadrant and x-axis.
Draw a rough sketch of the region {(x, y) : y2 ≤ 6ax and x 2 + y2 ≤ 16a2}. Also find the area of the region sketched using method of integration.
The area of the region bounded by the y-axis, y = cosx and y = sinx, 0 ≤ x ≤ `pi/2` is ______.
Area of the region bounded by the curve y = cosx between x = 0 and x = π is ______.
The area of the region bounded by the circle x2 + y2 = 1 is ______.
The area bounded by the curve `y = x^3`, the `x`-axis and ordinates `x` = – 2 and `x` = 1
Find the area of the region enclosed by the curves y2 = x, x = `1/4`, y = 0 and x = 1, using integration.
Find the area of the following region using integration ((x, y) : y2 ≤ 2x and y ≥ x – 4).
Make a rough sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 1, 0 ≤ y ≤ x + 1, 0 ≤ x ≤ 2} and find the area of the region, using the method of integration.
Find the area of the region bounded by the curve x2 = 4y and the line x = 4y – 2.
