Advertisements
Advertisements
प्रश्न
The area of the circle x2 + y2 = 16 enterior to the parabola y2 = 6x is
विकल्प
- \[\frac{4}{3}\left( 4\pi - \sqrt{3} \right)\]
- \[\frac{4}{3}\left( 4\pi + \sqrt{3} \right)\]
- \[\frac{4}{3}\left( 8\pi - \sqrt{3} \right)\]
- \[\frac{4}{3}\left( 8\pi + \sqrt{3} \right)\]
उत्तर

Points of intersection of the parabola and the circle is obtained by solving the simultaneous equations
\[x^2 + y^2 = 16\text{ and }y^2 = 6x\]
\[ \Rightarrow x^2 + 6x = 16 \]
\[ \Rightarrow x^2 + 6x - 16 = 0\]
\[ \Rightarrow \left( x + 8 \right)\left( x - 2 \right) = 0\]
\[ \Rightarrow x = 2\text{ or }x = - 8 \]
\[x\text{ can not be - 8 as in this case it will be the point outside circle . }\]
\[ \therefore x = 2\]
\[ \therefore\text{ When }x = 2, y = \pm \sqrt{6 \times 2} = \pm \sqrt{12} = \pm 2\sqrt{3}\]
\[ \therefore B\left( 2 , 2\sqrt{3} \right)\text{ and }B'\left( 2 , - 2\sqrt{3} \right)\text{ are points of intersection of the parabola and circle . }\]
\[\text{ Required area = Area }\left( OB'C'A'CBO \right) =\text{ area of circle - area }\left( OBAB'O \right) \]
\[\text{ Area of circle with radius }4 = \pi \times 4^2 = 16\pi \]
Now,
\[\text{ Area }\left( OBAB'O \right) = 2\text{ area }\left( OBAO \right)\]
\[ = 2\left[\text{ area }\left( OBDO \right) +\text{ area }\left( DBAD \right) \right]\]
\[ = 2 \times \left[ \int_0^2 \sqrt{6x} dx + \int_2^4 \sqrt{16 - x^2} dx \right]\]
\[ = 2 \times \left\{ \left[ \sqrt{6}\frac{x^\frac{3}{2}}{\frac{3}{2}} \right]_0^2 + \left[ \frac{x}{2}\sqrt{16 - x^2} + \frac{1}{2} \times 16 \sin^{- 1} \left( \frac{x}{4} \right) \right]_2^4 \right\}\]
\[ = 2 \times \left\{ \left( \sqrt{6} \times \frac{2}{3} \times 2^\frac{3}{2} - 0 \right) + \left( \frac{1}{2}4\sqrt{16 - \left( 4 \right)^2} + \frac{1}{2} \times 16 \sin^{- 1} \frac{4}{4} - \frac{2}{2}\sqrt{16 - 2^2} - \frac{1}{2} \times 16 \sin^{- 1} \frac{2}{4} \right) \right\}\]
\[ = 2 \times \left[ \left( \sqrt{6} \times \frac{2}{3} \times 2\sqrt{2} \right) + 0 + 8 \sin^{- 1} \left( 1 \right) - \sqrt{12} - 8 \sin^{- 1} \left( \frac{1}{2} \right) \right]\]
\[ = 2 \times \left[ \frac{8\sqrt{3}}{3} + 8 \times \frac{\pi}{2} - 2\sqrt{3} - 8\frac{\pi}{6} \right]\]
\[ = 2 \left\{ \frac{8\sqrt{3} - 6\sqrt{3}}{3} + 8\left( \frac{\pi}{2} - \frac{\pi}{6} \right) \right\}\]
\[ = 2\left\{ \frac{2\sqrt{3}}{3} + 8\left( \frac{2\pi}{6} \right) \right\}\]
\[ = \frac{4\sqrt{3}}{3} + \frac{16\pi}{3}\]
\[\text{ Shaded area }= 16\pi - \left( \frac{4\sqrt{3}}{3} + \frac{16\pi}{3} \right)\]
\[ = \frac{48\pi - 16\pi}{3} - \frac{4\sqrt{3}}{3}\]
\[ = \frac{32\pi}{3} - \frac{4\sqrt{3}}{3}\]
\[ = \frac{4}{3}\left( 8\pi - \sqrt{3} \right)\text{ sq units }\]
APPEARS IN
संबंधित प्रश्न
Find the area of ellipse `x^2/1 + y^2/4 = 1`
Find the area lying above the x-axis and under the parabola y = 4x − x2.
Find the area under the curve y = \[\sqrt{6x + 4}\] above x-axis from x = 0 to x = 2. Draw a sketch of curve also.
Sketch the graph y = | x − 5 |. Evaluate \[\int\limits_0^1 \left| x - 5 \right| dx\]. What does this value of the integral represent on the graph.
Draw a rough sketch of the curve y = \[\frac{\pi}{2} + 2 \sin^2 x\] and find the area between x-axis, the curve and the ordinates x = 0, x = π.
Find the area of the region bounded by x2 + 16y = 0 and its latusrectum.
Calculate the area of the region bounded by the parabolas y2 = x and x2 = y.
Using integration, find the area of the region bounded by the triangle ABC whose vertices A, B, C are (−1, 1), (0, 5) and (3, 2) respectively.
Draw a rough sketch of the region {(x, y) : y2 ≤ 5x, 5x2 + 5y2 ≤ 36} and find the area enclosed by the region using method of integration.
Find the area, lying above x-axis and included between the circle x2 + y2 = 8x and the parabola y2 = 4x.
Find the area of the region bounded by the curves y = x − 1 and (y − 1)2 = 4 (x + 1).
Using the method of integration, find the area of the region bounded by the following lines:
3x − y − 3 = 0, 2x + y − 12 = 0, x − 2y − 1 = 0.
Sketch the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 1. Also, find the area of this region.
Make a sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 3; 0 ≤ y ≤ 2x + 3; 0 ≤ x ≤ 3} and find its area using integration.
Find the area of the figure bounded by the curves y = | x − 1 | and y = 3 −| x |.
The area included between the parabolas y2 = 4x and x2 = 4y is (in square units)
Area bounded by parabola y2 = x and straight line 2y = x is _________ .
The area of the region (in square units) bounded by the curve x2 = 4y, line x = 2 and x-axis is
The area bounded by the curve y = f (x), x-axis, and the ordinates x = 1 and x = b is (b −1) sin (3b + 4). Then, f (x) is __________ .
Area bounded by the curve y = x3, the x-axis and the ordinates x = −2 and x = 1 is ______.
The area bounded by the y-axis, y = cos x and y = sin x when 0 ≤ x ≤ \[\frac{\pi}{2}\] is _________ .
Find the equation of the parabola with latus-rectum joining points (4, 6) and (4, -2).
Sketch the graphs of the curves y2 = x and y2 = 4 – 3x and find the area enclosed between them.
Using the method of integration, find the area of the region bounded by the lines 3x − 2y + 1 = 0, 2x + 3y − 21 = 0 and x − 5y + 9 = 0
Find the area of the curve y = sin x between 0 and π.
Find the area of the region bounded by the curve ay2 = x3, the y-axis and the lines y = a and y = 2a.
Find the area of the region bounded by the parabolas y2 = 6x and x2 = 6y.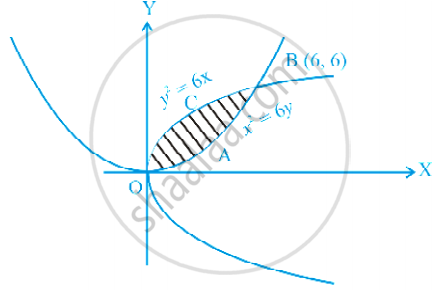
The area of the region bounded by the curve x = y2, y-axis and the line y = 3 and y = 4 is ______.
The area of the region bounded by the curve y = `sqrt(16 - x^2)` and x-axis is ______.
The area of the region bounded by the curve x = 2y + 3 and the y lines. y = 1 and y = –1 is ______.
Using integration, find the area of the region in the first quadrant enclosed by the line x + y = 2, the parabola y2 = x and the x-axis.
The region bounded by the curves `x = 1/2, x = 2, y = log x` and `y = 2^x`, then the area of this region, is
Find the area of the region bounded by `y^2 = 9x, x = 2, x = 4` and the `x`-axis in the first quadrant.
Find the area of the region bounded by curve 4x2 = y and the line y = 8x + 12, using integration.
Using integration, find the area bounded by the curve y2 = 4ax and the line x = a.
Sketch the region enclosed bounded by the curve, y = x |x| and the ordinates x = −1 and x = 1.
