Advertisements
Advertisements
प्रश्न
Draw a rough sketch of the region {(x, y) : y2 ≤ 5x, 5x2 + 5y2 ≤ 36} and find the area enclosed by the region using method of integration.
उत्तर
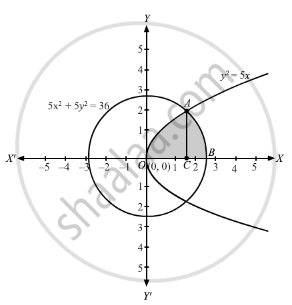
The given region is intersection of\[y^2 \leq 5x\text{ and }5 x^2 + 5 y^2 \leq 36\]
Clearly, \[y^2 \leq 5x\] is a parabola with vertex at origin and the axis is along the x-axis opening in the positive direction. Also \[5 x^2 + 5 y^2 \leq 36\] is a circle with centre at the origin and has a radius \[\sqrt{\frac{36}{5}}\text{ or }\frac{6}{\sqrt{5}}\]
Corresponding equations of given inequations are
\[y^2 = 5x . . . . . \left( 1 \right) \]
\[5 x^2 + 5 y^2 = 36 . . . . . \left( 2 \right)\]
Substituting the value of y2 from (1) into (2), we get
\[5 x^2 + 25x = 36\]
\[\Rightarrow 5 x^2 + 25x - 36 = 0\]
\[\Rightarrow x = \frac{- 25 \pm \sqrt{625 + 720}}{10}\]
\[\Rightarrow x = \frac{- 25 \pm \sqrt{1345}}{10}\]
From the figure we see that x-coordinate of intersecting point can not be negative.
\[\therefore x = \frac{- 25 + \sqrt{1345}}{10}\]
Now assume that x-coordinate of intersecting point, \[a = \frac{- 25 + \sqrt{1345}}{10}\]
The Required area, A = 2(Area of OACO + Area of CABC)
Approximating the area of OACO the length = | y1 |and a width = dx
\[\text{ Area of OACO }= \int_0^a \left| y_1 \right| d x\]
\[= \int_0^a y_1 d x\]
\[= \int_0^a \sqrt{5x} d x ............\left( \because {y_1}^2 = 5x \Rightarrow y_1 = \sqrt{5x} \right)\]
\[\sqrt{5} \left[ \frac{2 x^\frac{3}{2}}{3} \right]^a_0\]
Therefore, Area of OACO \[= \frac{2\sqrt{5} a^\frac{3}{2}}{3}\]
Similarly approximating the area of CABC the length \[=\left| y_2 \right|\] and the width = dx
\[\text{Area of CABC }= \int_a^\frac{6}{\sqrt{5}} \left| y_2 \right| d x\]
\[= \int_a^\frac{6}{\sqrt{5}} y_2 d x\]
Area of CABC\[= \frac{9\pi}{5} - \frac{a}{2}\sqrt{\frac{36}{5} - a^2} - \frac{18}{5} \sin^{- 1} \left( \frac{a\sqrt{5}}{6} \right)\]
Thus the Required area, A = 2(Area of OACO + Area of CABC)
APPEARS IN
संबंधित प्रश्न
Sketch the region bounded by the curves `y=sqrt(5-x^2)` and y=|x-1| and find its area using integration.
Find the area of the region bounded by the curve x2 = 16y, lines y = 2, y = 6 and Y-axis lying in the first quadrant.
Using the method of integration find the area of the region bounded by lines: 2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0
Area bounded by the curve y = x3, the x-axis and the ordinates x = –2 and x = 1 is ______.
Find the equation of a curve passing through the point (0, 2), given that the sum of the coordinates of any point on the curve exceeds the slope of the tangent to the curve at that point by 5
Find the area of the region bounded by the parabola y2 = 4ax and the line x = a.
Sketch the region {(x, y) : 9x2 + 4y2 = 36} and find the area of the region enclosed by it, using integration.
Using integration, find the area of the region bounded by the following curves, after making a rough sketch: y = 1 + | x + 1 |, x = −2, x = 3, y = 0.
Find the area of the region bounded by the curve xy − 3x − 2y − 10 = 0, x-axis and the lines x = 3, x = 4.
Find the area of the region bounded by the curve \[x = a t^2 , y = 2\text{ at }\]between the ordinates corresponding t = 1 and t = 2.
Find the area of the region common to the parabolas 4y2 = 9x and 3x2 = 16y.
Find the area of the region {(x, y) : y2 ≤ 8x, x2 + y2 ≤ 9}.
Draw a rough sketch of the region {(x, y) : y2 ≤ 3x, 3x2 + 3y2 ≤ 16} and find the area enclosed by the region using method of integration.
Find the area of the region bounded by \[y = \sqrt{x}, x = 2y + 3\] in the first quadrant and x-axis.
Find the area of the region bounded by \[y = \sqrt{x}\] and y = x.
Sketch the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 1. Also, find the area of this region.
Find the area of the region bounded by y = | x − 1 | and y = 1.
Find the area bounded by the lines y = 4x + 5, y = 5 − x and 4y = x + 5.
Find the area of the region between the parabola x = 4y − y2 and the line x = 2y − 3.
The area bounded by the curves y = sin x between the ordinates x = 0, x = π and the x-axis is _____________ .
Area bounded by parabola y2 = x and straight line 2y = x is _________ .
The area bounded by the curve y = 4x − x2 and the x-axis is __________ .
The area of the circle x2 + y2 = 16 enterior to the parabola y2 = 6x is
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using vertical strips.
Using integration, find the area of the smaller region bounded by the ellipse `"x"^2/9+"y"^2/4=1`and the line `"x"/3+"y"/2=1.`
The area enclosed by the ellipse `x^2/"a"^2 + y^2/"b"^2` = 1 is equal to ______.
Find the area enclosed by the curve y = –x2 and the straight lilne x + y + 2 = 0
Find the area of the region bounded by the curve y2 = 2x and x2 + y2 = 4x.
Compute the area bounded by the lines x + 2y = 2, y – x = 1 and 2x + y = 7.
Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32 is ______.
Let f(x) be a continuous function such that the area bounded by the curve y = f(x), x-axis and the lines x = 0 and x = a is `a^2/2 + a/2 sin a + pi/2 cos a`, then `f(pi/2)` =
Area of the region bounded by the curve `y^2 = 4x`, `y`-axis and the line `y` = 3 is:
Find the area of the region bounded by `x^2 = 4y, y = 2, y = 4`, and the `y`-axis in the first quadrant.
Let the curve y = y(x) be the solution of the differential equation, `("dy")/("d"x) = 2(x + 1)`. If the numerical value of area bounded by the curve y = y(x) and x-axis is `(4sqrt(8))/3`, then the value of y(1) is equal to ______.
Let f(x) be a non-negative continuous function such that the area bounded by the curve y = f(x), x-axis and the ordinates x = `π/4` and x = `β > π/4` is `(βsinβ + π/4 cos β + sqrt(2)β)`. Then `f(π/2)` is ______.
Sketch the region bounded by the lines 2x + y = 8, y = 2, y = 4 and the Y-axis. Hence, obtain its area using integration.
Sketch the region enclosed bounded by the curve, y = x |x| and the ordinates x = −1 and x = 1.
