Advertisements
Advertisements
प्रश्न
Find the area of the region {(x, y) : y2 ≤ 8x, x2 + y2 ≤ 9}.
उत्तर
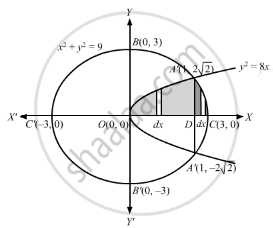
The point of intersection between the two curves is obtained by solving the two equations
APPEARS IN
संबंधित प्रश्न
Find the area bounded by the curve y2 = 4ax, x-axis and the lines x = 0 and x = a.
Sketch the graph y = | x + 3 |. Evaluate
Find the area of the region bounded by the curve xy − 3x − 2y − 10 = 0, x-axis and the lines x = 3, x = 4.
Compare the areas under the curves y = cos2 x and y = sin2 x between x = 0 and x = π.
Find the area bounded by the ellipse
Find the area of the region in the first quadrant bounded by the parabola y = 4x2 and the lines x = 0, y = 1 and y = 4.
Find the area of the region bounded by x2 = 16y, y = 1, y = 4 and the y-axis in the first quadrant.
Calculate the area of the region bounded by the parabolas y2 = x and x2 = y.
Find the area of the region bounded by the curves y = x − 1 and (y − 1)2 = 4 (x + 1).
Find the area enclosed by the curve
Find the area bounded by the parabola y = 2 − x2 and the straight line y + x = 0.
Using integration, find the area of the triangle ABC coordinates of whose vertices are A (4, 1), B (6, 6) and C (8, 4).
Find the area of the region bounded by y = | x − 1 | and y = 1.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2.
Make a sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 3; 0 ≤ y ≤ 2x + 3; 0 ≤ x ≤ 3} and find its area using integration.
Using integration, find the area of the following region:
The area bounded by y = 2 − x2 and x + y = 0 is _________ .
The area bounded by the parabola y2 = 4ax and x2 = 4ay is ___________ .
The area bounded by the curve y = 4x − x2 and the x-axis is __________ .
The area bounded by the parabola y2 = 8x, the x-axis and the latusrectum is ___________ .
The area bounded by the curve y = x |x| and the ordinates x = −1 and x = 1 is given by
Find the area of the region bounded by the curve ay2 = x3, the y-axis and the lines y = a and y = 2a.
The area of the region bounded by the curve x = y2, y-axis and the line y = 3 and y = 4 is ______.
Find the area of the region bounded by the parabola y2 = 2px, x2 = 2py
Using integration, find the area of the region bounded by the line 2y = 5x + 7, x- axis and the lines x = 2 and x = 8.
Draw a rough sketch of the region {(x, y) : y2 ≤ 6ax and x 2 + y2 ≤ 16a2}. Also find the area of the region sketched using method of integration.
Compute the area bounded by the lines x + 2y = 2, y – x = 1 and 2x + y = 7.
Find the area bounded by the lines y = 4x + 5, y = 5 – x and 4y = x + 5.
The area of the region bounded by the circle x2 + y2 = 1 is ______.
The area of the region bounded by the line y = 4 and the curve y = x2 is ______.
Find the area of the region bounded by the ellipse 
What is the area of the region bounded by the curve
Let g(x) = cosx2, f(x) =
Let P(x) be a real polynomial of degree 3 which vanishes at x = –3. Let P(x) have local minima at x = 1, local maxima at x = –1 and
The area (in square units) of the region bounded by the curves y + 2x2 = 0 and y + 3x2 = 1, is equal to ______.
Using integration, find the area of the region bounded by y = mx (m > 0), x = 1, x = 2 and the X-axis.
Sketch the region enclosed bounded by the curve, y = x |x| and the ordinates x = −1 and x = 1.
