Advertisements
Advertisements
प्रश्न
Find the area of the region bounded by the parabola y2 = 2px, x2 = 2py
उत्तर
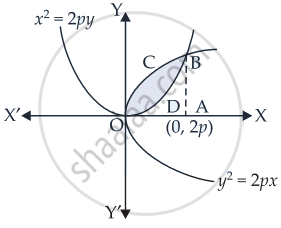
We are given that: x2 = 2py ......(i)
And y2 = 2px ......(ii)
From equation (i)
We get y = `x^2/(2"p")`
Putting the value of y in equation (ii)
We have `(x^2/(2"p"))` = 2px
⇒ `x^4/(4"p"^2)` = 2px
⇒ x4 = 8p3x
⇒ x4 – 8p3x = 0
⇒ x(x3 – 8p3) = 0
∴ x = 0, 2p
Required area = Area of the region (OCBA – ODBA)
= `int_0^(2"p") sqrt(2"p"x) "d"x - int_0^(2"p") x^2/(2"p") "d"x`
= `sqrt(2"p") * 2/3 [x^(3/2)]_0^(2"p") - 1/(2"p") * 1/3 [x^3]_0^(2"p")`
= `(2sqrt(2))/3 sqrt("p") [(2"p")^(3/2) - 0] - 1/(6"p") [(2"p")^3 - 0]`
= `(2sqrt(2))/3 sqrt("p") * 2sqrt(2) "p"^(3/2) - 1/(6"p") * 8"p"^3`
= `8/3 * "p"^2 - 8/6 "p"^2`
= `8/6 "p"^2`
= `4/3 "p"^2` sq.units
Hence, the required area = `4/3 "p"^2` sq.units
APPEARS IN
संबंधित प्रश्न
Find the area of the region bounded by the curve y = sinx, the lines x=-π/2 , x=π/2 and X-axis
Using the method of integration find the area of the region bounded by lines: 2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0
Using definite integrals, find the area of the circle x2 + y2 = a2.
Using integration, find the area of the region bounded by the following curves, after making a rough sketch: y = 1 + | x + 1 |, x = −2, x = 3, y = 0.
Draw a rough sketch of the curve \[y = \frac{x}{\pi} + 2 \sin^2 x\] and find the area between the x-axis, the curve and the ordinates x = 0 and x = π.
Find the area enclosed by the curve x = 3cost, y = 2sin t.
Find the area of the region bounded by x2 = 4ay and its latusrectum.
Calculate the area of the region bounded by the parabolas y2 = x and x2 = y.
Find the area bounded by the curve y = 4 − x2 and the lines y = 0, y = 3.
Find the area of the region in the first quadrant enclosed by x-axis, the line y = \[\sqrt{3}x\] and the circle x2 + y2 = 16.
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2= 32.
Find the area of the region between the parabola x = 4y − y2 and the line x = 2y − 3.
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using horizontal strips.
The area of the region formed by x2 + y2 − 6x − 4y + 12 ≤ 0, y ≤ x and x ≤ 5/2 is ______ .
The area bounded by the curve y = x4 − 2x3 + x2 + 3 with x-axis and ordinates corresponding to the minima of y is _________ .
The area of the region \[\left\{ \left( x, y \right) : x^2 + y^2 \leq 1 \leq x + y \right\}\] is __________ .
The area of the region bounded by the parabola y = x2 + 1 and the straight line x + y = 3 is given by
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices area A(1, 2), B (2, 0) and C (4, 3).
Draw a rough sketch of the curve y2 = 4x and find the area of region enclosed by the curve and the line y = x.
Find the area of the region bounded by the curve y = x3 and y = x + 6 and x = 0
Find the area enclosed by the curve y = –x2 and the straight lilne x + y + 2 = 0
Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32 is ______.
The area of the region bounded by the curve y = sinx between the ordinates x = 0, x = `pi/2` and the x-axis is ______.
Make a rough sketch of the region {(x, y): 0 ≤ y ≤ x2, 0 ≤ y ≤ x, 0 ≤ x ≤ 2} and find the area of the region using integration.
Area (in sq.units) of the region outside `|x|/2 + |y|/3` = 1 and inside the ellipse `x^2/4 + y^2/9` = 1 is ______.
Let f : [–2, 3] `rightarrow` [0, ∞) be a continuous function such that f(1 – x) = f(x) for all x ∈ [–2, 3]. If R1 is the numerical value of the area of the region bounded by y = f(x), x = –2, x = 3 and the axis of x and R2 = `int_-2^3 xf(x)dx`, then ______.
Using integration, find the area of the region bounded by line y = `sqrt(3)x`, the curve y = `sqrt(4 - x^2)` and Y-axis in first quadrant.
Find the area of the following region using integration ((x, y) : y2 ≤ 2x and y ≥ x – 4).
Evaluate:
`int_0^1x^2dx`
