Question

Calculate the area of the region bounded by the parabolas y² = x and x² = y.

Answer 1

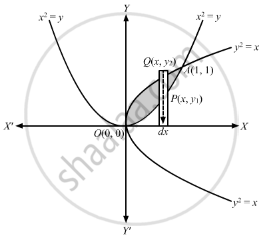
\[y^2 = x \text{ is a parabola, opening sideways, with vertex at O(0, 0) and + ve }x - \text{ axis as axis of symmetry }\]
\[ x^2 = y\text{ is a parabola, opening upwards, with vertex at O(0, 0) and + ve }y - \text{ axis as axis of symmetry }\]
Soving the above two equations, 
\[ x^2 = y^4 = y \]
\[ \Rightarrow y^4 - y = 0 \]
\[ \Rightarrow y = 0\text{ or }y = 1 . \]
\[So, x = 0\text{ or }x = 1\]
\[ \Rightarrow\text{ O }\left( 0, 0 \right) \text{ and }A(1, 1)\text{ are points of intersection of two curves }\]
\[\text{ Consider a vertical strip of length }= \left| y_2 - y_1 \right|\text{ and width }= dx \]
\[ \Rightarrow \text{ Area of approximating rectangle }= \left| y_2 - y_1 \right| dx \]
\[\text{ Approximating rectangle moves from }x = 0 \text{ to }x = 1\]
\[ \Rightarrow\text{ Area of the shaded region }= \int_0^1 \left| y_2 - y_1 \right| dx \]
\[ \Rightarrow A = \int_0^1 \left( y_2 - y_1 \right) dx ...................\left[ As, y_2 - y_1 > 0 \Rightarrow \left| y_2 - y_1 \right| = y_1 \right]\]
\[ \Rightarrow A = \int_0^1 \left( \sqrt{x} - x^2 \right) dx \]
\[ \Rightarrow A = \left[ \frac{x^\frac{3}{2}}{\frac{3}{2}} - \frac{x^3}{3} \right]_0^1 \]
\[ \Rightarrow A = \left[ \frac{2}{3} \times 1^\frac{3}{2} - \frac{1^3}{3} - 0 \right]\]
\[ \Rightarrow A = \frac{2}{3} - \frac{1}{3}\]
\[ \Rightarrow A = \frac{1}{3}\text{ sq . units }\]
\[\text{ Thus, area enclosed by the curves }= \frac{1}{3}\text{ sq . units }\]