Advertisements
Advertisements
प्रश्न
Find the area of the region above the x-axis, included between the parabola y2 = ax and the circle x2 + y2 = 2ax.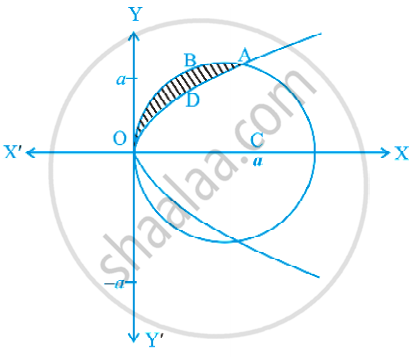
उत्तर
Solving the given equations of curves
We have x2 + ax = 2ax or x = 0, x = a
Which give y = 0.
y = ±a
From the figure in the question
Area ODAB = `int_0^"a" (sqrt(2"a"x - x^2) - sqrt("a"x))"d"x`
Let x = 2a sin2θ.
Then dx = 4a sinθ cosθ dθ and x = 0
⇒ θ = 0, x = a
⇒ θ = `pi/4`.
Again, `int_0"a" sqrt(2"a"x - x^2) "d"x = int_0^(pi/4) (2"a" sintheta costheta)(4"a" sintheta costheta)"d"theta`
= `"a"^2 int_0^(pi/4) (1 - cos 4theta) "d"theta`
= `"a"^2(theta - (sin 4theta)/4)_0^(pi/4)`
= `pi/4 "a"^2`.
Further more,
`int_0^"a" sqrt("a"x) "d"x = sqrt("a") 2/3 (x^(3/2))_0^"a"`
= `2/3 "a"^2`
Thus the required area = `pi/4 "a"^2 - 2/3 "a"^2`
= `"a"^2 (pi/4 - 2/3)` sq.units
APPEARS IN
संबंधित प्रश्न
triangle bounded by the lines y = 0, y = x and x = 4 is revolved about the X-axis. Find the volume of the solid of revolution.
Find the area of the region lying in the first quandrant bounded by the curve y2= 4x, X axis and the lines x = 1, x = 4
Draw the rough sketch of y2 + 1 = x, x ≤ 2. Find the area enclosed by the curve and the line x = 2.
Using integration, find the area of the region bounded by the line 2y = 5x + 7, x-axis and the lines x = 2 and x = 8.
Draw a rough sketch of the curve y = \[\frac{\pi}{2} + 2 \sin^2 x\] and find the area between x-axis, the curve and the ordinates x = 0, x = π.
Find the area of the region in the first quadrant bounded by the parabola y = 4x2 and the lines x = 0, y = 1 and y = 4.
Find the area bounded by the curve y = 4 − x2 and the lines y = 0, y = 3.
Find the area, lying above x-axis and included between the circle x2 + y2 = 8x and the parabola y2 = 4x.
Using the method of integration, find the area of the region bounded by the following lines:
3x − y − 3 = 0, 2x + y − 12 = 0, x − 2y − 1 = 0.
Using integration find the area of the region:
\[\left\{ \left( x, y \right) : \left| x - 1 \right| \leq y \leq \sqrt{5 - x^2} \right\}\]
Find the area of the region bounded by y = | x − 1 | and y = 1.
Make a sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 3; 0 ≤ y ≤ 2x + 3; 0 ≤ x ≤ 3} and find its area using integration.
Find the area of the region bounded by the parabola y2 = 2x and the straight line x − y = 4.
The area of the region bounded by the parabola y = x2 + 1 and the straight line x + y = 3 is given by
Draw a rough sketch of the curve y2 = 4x and find the area of region enclosed by the curve and the line y = x.
The area of the region bounded by the curve y = x2 and the line y = 16 ______.
Find the area of the region bounded by the curves y2 = 9x, y = 3x
Find the area of the region included between y2 = 9x and y = x
The area of the region bounded by the ellipse `x^2/25 + y^2/16` = 1 is ______.
If a and c are positive real numbers and the ellipse `x^2/(4c^2) + y^2/c^2` = 1 has four distinct points in common with the circle `x^2 + y^2 = 9a^2`, then
Area lying in the first quadrant and bounded by the circle `x^2 + y^2 = 4` and the lines `x + 0` and `x = 2`.
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9` = 1.
Using integration, find the area of the region bounded by the curves x2 + y2 = 4, x = `sqrt(3)`y and x-axis lying in the first quadrant.
The area enclosed by y2 = 8x and y = `sqrt(2x)` that lies outside the triangle formed by y = `sqrt(2x)`, x = 1, y = `2sqrt(2)`, is equal to ______.
Area of figure bounded by straight lines x = 0, x = 2 and the curves y = 2x, y = 2x – x2 is ______.
Let g(x) = cosx2, f(x) = `sqrt(x)`, and α, β (α < β) be the roots of the quadratic equation 18x2 – 9πx + π2 = 0. Then the area (in sq. units) bounded by the curve y = (gof)(x) and the lines x = α, x = β and y = 0, is ______.
Make a rough sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 1, 0 ≤ y ≤ x + 1, 0 ≤ x ≤ 2} and find the area of the region, using the method of integration.
Evaluate:
`int_0^1x^2dx`
