Advertisements
Advertisements
प्रश्न
Find the area of region bounded by the line x = 2 and the parabola y2 = 8x
उत्तर
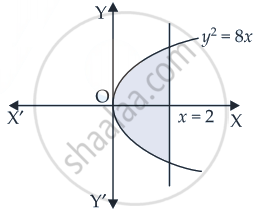
Here, y2 = 8x and x = 2
y2 = 8(2) = 16
∴ y = ±4
Required area = `2 int_0^2 sqrt(8x) "d"x`
= `2 xx 2sqrt(2) int_0^2 sqrt(x) "d"x`
= `4sqrt(2) xx 2/3 [x^(3/2)]_0^2`
= `(8sqrt(2))/3 [(2)^(3/2)]`
= `(8sqrt(2))/3 xx 2sqrt(2)`
= `32/3` sq.units
Hence, the area of the region = `32/3` sq.units
APPEARS IN
संबंधित प्रश्न
Find the area bounded by the curve y2 = 4ax, x-axis and the lines x = 0 and x = a.
Prove that the curves y2 = 4x and x2 = 4y divide the area of square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.
Using integration, find the area of the region bounded by the lines y = 2 + x, y = 2 – x and x = 2.
Using the method of integration, find the area of the triangular region whose vertices are (2, -2), (4, 3) and (1, 2).
Sketch the region bounded by the curves `y=sqrt(5-x^2)` and y=|x-1| and find its area using integration.
Draw a rough sketch to indicate the region bounded between the curve y2 = 4x and the line x = 3. Also, find the area of this region.
Using integration, find the area of the region bounded by the following curves, after making a rough sketch: y = 1 + | x + 1 |, x = −2, x = 3, y = 0.
Find the area of the region bounded by x2 + 16y = 0 and its latusrectum.
Find the area of the region bounded by the curve \[a y^2 = x^3\], the y-axis and the lines y = a and y = 2a.
Find the area of the region bounded by y =\[\sqrt{x}\] and y = x.
Find the area of the region {(x, y): x2 + y2 ≤ 4, x + y ≥ 2}.
Using integration, find the area of the following region: \[\left\{ \left( x, y \right) : \frac{x^2}{9} + \frac{y^2}{4} \leq 1 \leq \frac{x}{3} + \frac{y}{2} \right\}\]
The closed area made by the parabola y = 2x2 and y = x2 + 4 is __________ .
Area bounded by parabola y2 = x and straight line 2y = x is _________ .
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using vertical strips.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2
Find the area of the region bounded by y = `sqrt(x)` and y = x.
Area of the region bounded by the curve y = cosx between x = 0 and x = π is ______.
The area of the region bounded by the curve y = sinx between the ordinates x = 0, x = `pi/2` and the x-axis is ______.
The area of the region bounded by the curve y = x + 1 and the lines x = 2 and x = 3 is ______.
Using integration, find the area of the region bounded between the line x = 4 and the parabola y2 = 16x.
Smaller area bounded by the circle `x^2 + y^2 = 4` and the line `x + y = 2` is.
The area bounded by the curve `y = x|x|`, `x`-axis and the ordinate `x` = – 1 and `x` = 1 is given by
The area (in square units) of the region bounded by the curves y + 2x2 = 0 and y + 3x2 = 1, is equal to ______.
Find the area of the following region using integration ((x, y) : y2 ≤ 2x and y ≥ x – 4).
Make a rough sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 1, 0 ≤ y ≤ x + 1, 0 ≤ x ≤ 2} and find the area of the region, using the method of integration.
Using integration, find the area bounded by the curve y2 = 4ax and the line x = a.
Using integration, find the area of the region bounded by the curve y2 = 4x and x2 = 4y.
