Advertisements
Advertisements
प्रश्न
Using integration, find the area of the region bounded by the curve y2 = 4x and x2 = 4y.
उत्तर
Given that the curves are y2 = 4x and x2 = 4y.
Now, the graph of the provided curves is as follows:
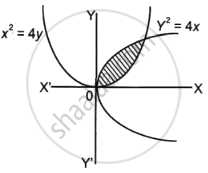
The given equations are:
y2 = 4x ...(i)
And x2 = 4y
`y = x^2/4` ...(ii)
Put the value of (ii) in (i), we get
`(x^2/4)^2 = 4x`
`\implies x^4/16 = 4x`
`\implies` x4 = 4 × 16x
`\implies` x4 – 64x = 0
`\implies` x(x3 – 64) = 0
`\implies` x = 0 or x = 4
The curve is rewritten as follows:
y2 = 4x
`\implies y = sqrt(4x) = 2sqrt(x)`
`\implies` x2 = 4y
`\implies y = x^2/4`
Now, the area of the bounded region is given as:
A = `int_0^4 (2sqrt(x) - x^2/4)dx`
= `[2 xx x^(3/2)/(3/2) - x^3/12]_0^4`
= `[(4/3 xx 4^(3//2)) - 4^3/12] - 0`
= `[(4 xx 8)/3 - 64/12]`
= `(128 - 64)/12`
= `64/12`
= `16/3` sq.units
APPEARS IN
संबंधित प्रश्न
Find the area of the region bounded by the curve x2 = 16y, lines y = 2, y = 6 and Y-axis lying in the first quadrant.
Draw a rough sketch to indicate the region bounded between the curve y2 = 4x and the line x = 3. Also, find the area of this region.
Make a rough sketch of the graph of the function y = 4 − x2, 0 ≤ x ≤ 2 and determine the area enclosed by the curve, the x-axis and the lines x = 0 and x = 2.
Find the area of the region bounded by the curve xy − 3x − 2y − 10 = 0, x-axis and the lines x = 3, x = 4.
Find the area bounded by the ellipse \[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\] and the ordinates x = ae and x = 0, where b2 = a2 (1 − e2) and e < 1.
Find the area of the minor segment of the circle \[x^2 + y^2 = a^2\] cut off by the line \[x = \frac{a}{2}\]
Find the area of the region bounded by x2 = 16y, y = 1, y = 4 and the y-axis in the first quadrant.
Find the area of the region bounded by the curve \[a y^2 = x^3\], the y-axis and the lines y = a and y = 2a.
Find the area of the region bounded by y =\[\sqrt{x}\] and y = x.
Find the area bounded by the curve y = 4 − x2 and the lines y = 0, y = 3.
Find the area of the region bounded by \[y = \sqrt{x}, x = 2y + 3\] in the first quadrant and x-axis.
Find the area common to the circle x2 + y2 = 16 a2 and the parabola y2 = 6 ax.
OR
Find the area of the region {(x, y) : y2 ≤ 6ax} and {(x, y) : x2 + y2 ≤ 16a2}.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2.
Find the area enclosed by the curves y = | x − 1 | and y = −| x − 1 | + 1.
Find the area enclosed by the parabolas y = 4x − x2 and y = x2 − x.
Find the area bounded by the parabola x = 8 + 2y − y2; the y-axis and the lines y = −1 and y = 3.
The area of the region bounded by the parabola y = x2 + 1 and the straight line x + y = 3 is given by
The area of the region (in square units) bounded by the curve x2 = 4y, line x = 2 and x-axis is
Draw a rough sketch of the curve y2 = 4x and find the area of region enclosed by the curve and the line y = x.
Find the area of the region bound by the curves y = 6x – x2 and y = x2 – 2x
Find the area bounded by the lines y = 4x + 5, y = 5 – x and 4y = x + 5.
The region bounded by the curves `x = 1/2, x = 2, y = log x` and `y = 2^x`, then the area of this region, is
Find the area of the region bounded by the curve `y^2 - x` and the line `x` = 1, `x` = 4 and the `x`-axis.
Find the area of the region bounded by the curve `y = x^2 + 2, y = x, x = 0` and `x = 3`
The area bounded by the curve `y = x^3`, the `x`-axis and ordinates `x` = – 2 and `x` = 1
Let the curve y = y(x) be the solution of the differential equation, `("dy")/("d"x) = 2(x + 1)`. If the numerical value of area bounded by the curve y = y(x) and x-axis is `(4sqrt(8))/3`, then the value of y(1) is equal to ______.
Let f(x) be a non-negative continuous function such that the area bounded by the curve y = f(x), x-axis and the ordinates x = `π/4` and x = `β > π/4` is `(βsinβ + π/4 cos β + sqrt(2)β)`. Then `f(π/2)` is ______.
Let P(x) be a real polynomial of degree 3 which vanishes at x = –3. Let P(x) have local minima at x = 1, local maxima at x = –1 and `int_-1^1 P(x)dx` = 18, then the sum of all the coefficients of the polynomial P(x) is equal to ______.
Using integration, find the area of the region bounded by line y = `sqrt(3)x`, the curve y = `sqrt(4 - x^2)` and Y-axis in first quadrant.
Find the area of the following region using integration ((x, y) : y2 ≤ 2x and y ≥ x – 4).
