Advertisements
Advertisements
प्रश्न
Find the area enclosed by the curves y = | x − 1 | and y = −| x − 1 | + 1.
उत्तर
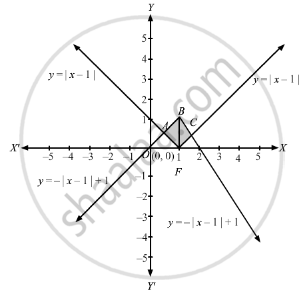
The given curves are \[y = \left| x - 1 \right| . . . . . \left( 1 \right)\]
\[y = - \left| x - 1 \right| + 1 . . . . . \left( 2 \right)\]
Clearly \[y = \left| x - 1 \right|\] is cutting the x-axis at (1, 0) and the y-axis at (0, 1) respectively.
Also \[y = - \left| x - 1 \right| + 1\] is cutting both the axes at (0, 0) and x-axis at (2, 0).
We have,
\[y = \left| x - 1 \right|\]
\[y = \begin{cases}x - 1& x \geq 1\\1 - x& x < 1\end{cases}\]
And
\[y = - \left| x - 1 \right| + 1\]
\[y = \begin{cases}2 - x &x \geq 1\\ x &x < 1\end{cases}\]
\[\text{ Solving both the equations for }x < 1\]
\[y = 1 - x\text{ and }y = x, \]
\[\text{ We get }x = \frac{1}{2}\text{ and }y = \frac{1}{2}\]
\[\text{ And solving both the equations for }x \geq 1\]
\[y = x - 1\text{ and }y = 2 - x, \]
\[\text{ We get }x = \frac{3}{2}\text{ and }y = \frac{1}{2}\]
Thus the intersecting points are \[\left( \frac{1}{2}, \frac{1}{2} \right)\] and \[\left( \frac{3}{2}, \frac{1}{2} \right)\]
The required area A = ( Area of ABFA + Area of BCFB)
Now approximating the area of ABFA the length = \[\left| y_1 \right|\] and width = dx
Area of ABFA
\[= \int_\frac{1}{2}^1 \left[ x - \left( 1 - x \right) \right] d x\]
\[ = \int_\frac{1}{2}^1 \left( 2x - 1 \right) d x\]
\[ = \left[ x^2 - x \right]_\frac{1}{2}^1 \]
\[ = \frac{1}{4}\]
Similarly approximating the area of BCFB the length \[= \left| y_2 \right|\] and width= dx
Area of BCFB
\[= \int_1^\frac{3}{2} \left[ \left( 2 - x \right) - \left( x - 1 \right) \right] d x\]
\[ = \int_1^\frac{3}{2} \left( 3 - 2x \right) d x\]
\[ = \left[ 3x - x^2 \right]_1^\frac{3}{2} \]
\[ = \frac{1}{4}\]
Thus the required area A =( Area of ABFA + Area of BCFB)
Hence the required area is \[\frac{1}{2}\] square units.
APPEARS IN
संबंधित प्रश्न
Find the area of ellipse `x^2/1 + y^2/4 = 1`
Draw a rough sketch of the curve and find the area of the region bounded by curve y2 = 8x and the line x =2.
Sketch the region {(x, y) : 9x2 + 4y2 = 36} and find the area of the region enclosed by it, using integration.
Sketch the graph y = | x + 1 |. Evaluate\[\int\limits_{- 4}^2 \left| x + 1 \right| dx\]. What does the value of this integral represent on the graph?
Find the area of the region bounded by the curve xy − 3x − 2y − 10 = 0, x-axis and the lines x = 3, x = 4.
Draw a rough sketch of the curve \[y = \frac{x}{\pi} + 2 \sin^2 x\] and find the area between the x-axis, the curve and the ordinates x = 0 and x = π.
Find the area of the region bounded by x2 = 16y, y = 1, y = 4 and the y-axis in the first quadrant.
Calculate the area of the region bounded by the parabolas y2 = x and x2 = y.
Find the area of the region common to the parabolas 4y2 = 9x and 3x2 = 16y.
Find the area bounded by the curve y = 4 − x2 and the lines y = 0, y = 3.
Using integration, find the area of the region bounded by the triangle whose vertices are (2, 1), (3, 4) and (5, 2).
Using integration, find the area of the triangular region, the equations of whose sides are y = 2x + 1, y = 3x+ 1 and x = 4.
Draw a rough sketch of the region {(x, y) : y2 ≤ 5x, 5x2 + 5y2 ≤ 36} and find the area enclosed by the region using method of integration.
Find the area of the region in the first quadrant enclosed by x-axis, the line y = \[\sqrt{3}x\] and the circle x2 + y2 = 16.
Find the area bounded by the parabola y = 2 − x2 and the straight line y + x = 0.
Sketch the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 1. Also, find the area of this region.
Find the area bounded by the curves x = y2 and x = 3 − 2y2.
Find the area of the region bounded by y = | x − 1 | and y = 1.
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2= 32.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2.
Find the area of the region {(x, y): x2 + y2 ≤ 4, x + y ≥ 2}.
If the area above the x-axis, bounded by the curves y = 2kx and x = 0, and x = 2 is \[\frac{3}{\log_e 2}\], then the value of k is __________ .
The area included between the parabolas y2 = 4x and x2 = 4y is (in square units)
The area bounded by the parabola x = 4 − y2 and y-axis, in square units, is ____________ .
The closed area made by the parabola y = 2x2 and y = x2 + 4 is __________ .
The area bounded by the curve y2 = 8x and x2 = 8y is ___________ .
Find the coordinates of a point of the parabola y = x2 + 7x + 2 which is closest to the straight line y = 3x − 3.
Find the area of the region included between y2 = 9x and y = x
Find the area bounded by the curve y = `sqrt(x)`, x = 2y + 3 in the first quadrant and x-axis.
Find the area of the region bounded by the curve y2 = 2x and x2 + y2 = 4x.
Area of the region bounded by the curve y = cosx between x = 0 and x = π is ______.
The area of the region bounded by the ellipse `x^2/25 + y^2/16` = 1 is ______.
Using integration, find the area of the region `{(x, y): 0 ≤ y ≤ sqrt(3)x, x^2 + y^2 ≤ 4}`
The region bounded by the curves `x = 1/2, x = 2, y = log x` and `y = 2^x`, then the area of this region, is
Find the area of the region bounded by the curve `y = x^2 + 2, y = x, x = 0` and `x = 3`
The area (in sq.units) of the region A = {(x, y) ∈ R × R/0 ≤ x ≤ 3, 0 ≤ y ≤ 4, y ≤x2 + 3x} is ______.
Let g(x) = cosx2, f(x) = `sqrt(x)`, and α, β (α < β) be the roots of the quadratic equation 18x2 – 9πx + π2 = 0. Then the area (in sq. units) bounded by the curve y = (gof)(x) and the lines x = α, x = β and y = 0, is ______.
