Question

The area bounded by the parabola x = 4 − y² and y-axis, in square units, is ____________ .

विकल्प

• \[\frac{3}{32}\]

• \[\frac{32}{3}\]

• \[\frac{33}{2}\]

• \[\frac{16}{3}\]

Answer 1

\[\frac{32}{3}\]

 

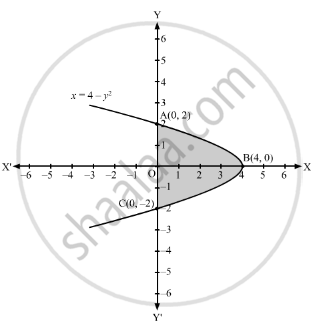
The points of intersection of the parabola and the y-axis are A(0, 2) and C(0, −2).
Therefore, the area of the required region ABCO,
\[A = \int_{- 2}^2 x d y\]
\[ = \int_{- 2}^2 \left( 4 - y^2 \right) d y\]
\[ = \left[ 4y - \frac{y^3}{3} \right]_{- 2}^2 \]
\[ = \left[ 4\left( 2 \right) - \frac{\left( 2 \right)^3}{3} \right] - \left[ 4\left( - 2 \right) - \frac{\left( - 2 \right)^3}{3} \right]\]
\[ = \left( 8 - \frac{8}{3} \right) - \left( - 8 + \frac{8}{3} \right)\]
\[ = 8 - \frac{8}{3} + 8 - \frac{8}{3}\]
\[ = 16 - \frac{16}{3}\]
\[ = \frac{32}{3}\text{ square units }\]