Advertisements
Advertisements
प्रश्न
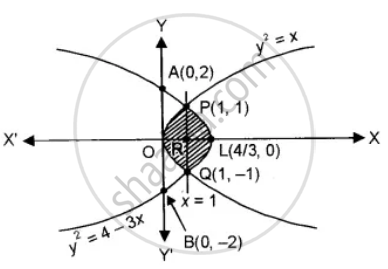
Sketch the graphs of the curves y2 = x and y2 = 4 – 3x and find the area enclosed between them.
उत्तर
y2 = -3x + 4
= - 3 `( x - (4)/(3))`
The vertex L of this parabola is `((4)/(3),0)`.
It cuts the y-axis at A (0, 2) and B (0, - 2).
The points of intersection of these two parabolas are given by the equation
y2 = x and y2 = 4 - 3x as x = - 3x + 4 ⇒ x = 1
Then y2 = 1 ⇒ y = ± 1
Thus, the points of intersection are P (1, 1) and Q (1, - 1). Let PQ cut the x-axis at R.
∴ Total area of POQLP = 2 area of OPRQO
= 2 `[ int_0^1sqrtx dx + int_1^(4/3) sqrt(4 - 3x) dx]`
= 2`[ (( x^(3/2)) /(3/2))_0^1 + ((2(4 - 3x))/((-3) xx 3))_1^(4/3)]`
= 2`[ ((2)/(3) - 0) - (2)/(9) (0 - 1)]`
= 2`[(2)/(3) + (2)/(9)] = 2 [ (6 + 2)/(9)]`
= `(16)/(9)` sq. units
APPEARS IN
संबंधित प्रश्न
Using the method of integration find the area of the region bounded by lines: 2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0
Find the area lying above the x-axis and under the parabola y = 4x − x2.
Sketch the graph y = | x − 5 |. Evaluate \[\int\limits_0^1 \left| x - 5 \right| dx\]. What does this value of the integral represent on the graph.
Find the area of the region in the first quadrant bounded by the parabola y = 4x2 and the lines x = 0, y = 1 and y = 4.
Find the area of the region bounded by x2 + 16y = 0 and its latusrectum.
Find the area of the region bounded by y =\[\sqrt{x}\] and y = x.
Draw a rough sketch of the region {(x, y) : y2 ≤ 5x, 5x2 + 5y2 ≤ 36} and find the area enclosed by the region using method of integration.
Find the area of the region bounded by the parabola y2 = 2x + 1 and the line x − y − 1 = 0.
Using the method of integration, find the area of the region bounded by the following lines:
3x − y − 3 = 0, 2x + y − 12 = 0, x − 2y − 1 = 0.
Using integration, find the area of the triangle ABC coordinates of whose vertices are A (4, 1), B (6, 6) and C (8, 4).
Using integration find the area of the region:
\[\left\{ \left( x, y \right) : \left| x - 1 \right| \leq y \leq \sqrt{5 - x^2} \right\}\]
Make a sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 3; 0 ≤ y ≤ 2x + 3; 0 ≤ x ≤ 3} and find its area using integration.
Find the area bounded by the lines y = 4x + 5, y = 5 − x and 4y = x + 5.
Find the area of the region {(x, y): x2 + y2 ≤ 4, x + y ≥ 2}.
Find the area enclosed by the curves y = | x − 1 | and y = −| x − 1 | + 1.
Find the area of the figure bounded by the curves y = | x − 1 | and y = 3 −| x |.
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using horizontal strips.
If An be the area bounded by the curve y = (tan x)n and the lines x = 0, y = 0 and x = π/4, then for x > 2
The area of the region \[\left\{ \left( x, y \right) : x^2 + y^2 \leq 1 \leq x + y \right\}\] is __________ .
The area bounded by the curve y = f (x), x-axis, and the ordinates x = 1 and x = b is (b −1) sin (3b + 4). Then, f (x) is __________ .
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices area A(1, 2), B (2, 0) and C (4, 3).
Draw a rough sketch of the curve y2 = 4x and find the area of region enclosed by the curve and the line y = x.
Find the area of the region bounded by the parabola y2 = 2x and the straight line x – y = 4.
The area enclosed by the ellipse `x^2/"a"^2 + y^2/"b"^2` = 1 is equal to ______.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2
The area of the region bounded by the curve y = x + 1 and the lines x = 2 and x = 3 is ______.
The area of the region bounded by the line y = 4 and the curve y = x2 is ______.
The area bounded by the curve `y = x|x|`, `x`-axis and the ordinate `x` = – 1 and `x` = 1 is given by
Using integration, find the area of the region bounded by the curves x2 + y2 = 4, x = `sqrt(3)`y and x-axis lying in the first quadrant.
Evaluate:
`int_0^1x^2dx`
