Advertisements
Advertisements
प्रश्न
The area bounded by the curve y = loge x and x-axis and the straight line x = e is ___________ .
विकल्प
e sq. units
1 sq. units
1−\[\frac{1}{e}\] sq. units
1+\[\frac{1}{e}\] sq. units
उत्तर
1 sq. units
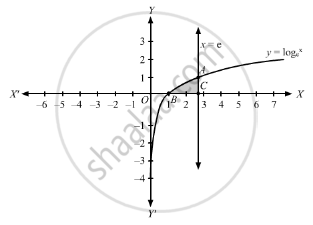
The point of intersection of the curve and the straight line is A(e, 1).
Therefore, the area of the required region ABC,
\[A = \int_0^1 \left( x_1 - x_2 \right) d y ..........\left(\text{ where, }x_1 = e\text{ and }x_2 = e^y \right)\]
\[ = \int_0^1 \left( e - e^y \right) d y\]
\[ = \left[ ey - e^y \right]_0^1 \]
\[ = \left\{ e\left( 1 \right) - e^\left( 1 \right) \right\} - \left\{ e\left( 0 \right) - e^\left( 0 \right) \right\}\]
\[ = e - e + 1\]
\[ = 1\text{ square unit }\]
APPEARS IN
संबंधित प्रश्न
triangle bounded by the lines y = 0, y = x and x = 4 is revolved about the X-axis. Find the volume of the solid of revolution.
Find the area of the region common to the circle x2 + y2 =9 and the parabola y2 =8x
Find the area of the sector of a circle bounded by the circle x2 + y2 = 16 and the line y = x in the ftrst quadrant.
Find the area of the region lying in the first quandrant bounded by the curve y2= 4x, X axis and the lines x = 1, x = 4
Find the area of ellipse `x^2/1 + y^2/4 = 1`
Sketch the graph of y = |x + 4|. Using integration, find the area of the region bounded by the curve y = |x + 4| and x = –6 and x = 0.
Find the area lying above the x-axis and under the parabola y = 4x − x2.
Sketch the region {(x, y) : 9x2 + 4y2 = 36} and find the area of the region enclosed by it, using integration.
Determine the area under the curve y = \[\sqrt{a^2 - x^2}\] included between the lines x = 0 and x = a.
Show that the areas under the curves y = sin x and y = sin 2x between x = 0 and x =\[\frac{\pi}{3}\] are in the ratio 2 : 3.
Find the area of the region common to the parabolas 4y2 = 9x and 3x2 = 16y.
Find the area of the region bounded by y =\[\sqrt{x}\] and y = x.
Using integration, find the area of the region bounded by the triangle whose vertices are (2, 1), (3, 4) and (5, 2).
Find the area of the region bounded by \[y = \sqrt{x}, x = 2y + 3\] in the first quadrant and x-axis.
Find the area bounded by the parabola y = 2 − x2 and the straight line y + x = 0.
Find the area bounded by the curves x = y2 and x = 3 − 2y2.
Find the area of the circle x2 + y2 = 16 which is exterior to the parabola y2 = 6x.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2.
Find the area bounded by the lines y = 4x + 5, y = 5 − x and 4y = x + 5.
Find the area enclosed by the curves 3x2 + 5y = 32 and y = | x − 2 |.
Find the area of the region bounded by the parabola y2 = 2x and the straight line x − y = 4.
The area bounded by the curves y = sin x between the ordinates x = 0, x = π and the x-axis is _____________ .
The area bounded by the curve y = 4x − x2 and the x-axis is __________ .
The area enclosed by the circle x2 + y2 = 2 is equal to ______.
Find the area of the region bounded by the curves y2 = 9x, y = 3x
Find the area of the region bounded by the curve y2 = 4x, x2 = 4y.
Find the area of the region included between y2 = 9x and y = x
Sketch the region `{(x, 0) : y = sqrt(4 - x^2)}` and x-axis. Find the area of the region using integration.
Find the area bounded by the curve y = sinx between x = 0 and x = 2π.
Compute the area bounded by the lines x + 2y = 2, y – x = 1 and 2x + y = 7.
Area of the region bounded by the curve y = cosx between x = 0 and x = π is ______.
Let f(x) be a continuous function such that the area bounded by the curve y = f(x), x-axis and the lines x = 0 and x = a is `a^2/2 + a/2 sin a + pi/2 cos a`, then `f(pi/2)` =
Find the area of the region bounded by the curve `y = x^2 + 2, y = x, x = 0` and `x = 3`
Find the area bounded by the curve y = |x – 1| and y = 1, using integration.
The area of the region bounded by the parabola (y – 2)2 = (x – 1), the tangent to it at the point whose ordinate is 3 and the x-axis is ______.
