Advertisements
Advertisements
प्रश्न
Draw a rough sketch of the region {(x, y) : y2 ≤ 5x, 5x2 + 5y2 ≤ 36} and find the area enclosed by the region using method of integration.
उत्तर
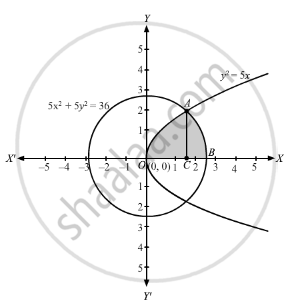
The given region is intersection of\[y^2 \leq 5x\text{ and }5 x^2 + 5 y^2 \leq 36\]
Clearly, \[y^2 \leq 5x\] is a parabola with vertex at origin and the axis is along the x-axis opening in the positive direction. Also \[5 x^2 + 5 y^2 \leq 36\] is a circle with centre at the origin and has a radius \[\sqrt{\frac{36}{5}}\text{ or }\frac{6}{\sqrt{5}}\]
Corresponding equations of given inequations are
\[y^2 = 5x . . . . . \left( 1 \right) \]
\[5 x^2 + 5 y^2 = 36 . . . . . \left( 2 \right)\]
Substituting the value of y2 from (1) into (2), we get
\[5 x^2 + 25x = 36\]
\[\Rightarrow 5 x^2 + 25x - 36 = 0\]
\[\Rightarrow x = \frac{- 25 \pm \sqrt{625 + 720}}{10}\]
\[\Rightarrow x = \frac{- 25 \pm \sqrt{1345}}{10}\]
From the figure we see that x-coordinate of intersecting point can not be negative.
\[\therefore x = \frac{- 25 + \sqrt{1345}}{10}\]
Now assume that x-coordinate of intersecting point, \[a = \frac{- 25 + \sqrt{1345}}{10}\]
The Required area, A = 2(Area of OACO + Area of CABC)
Approximating the area of OACO the length = | y1 |and a width = dx
\[\text{ Area of OACO }= \int_0^a \left| y_1 \right| d x\]
\[= \int_0^a y_1 d x\]
\[= \int_0^a \sqrt{5x} d x ............\left( \because {y_1}^2 = 5x \Rightarrow y_1 = \sqrt{5x} \right)\]
\[\sqrt{5} \left[ \frac{2 x^\frac{3}{2}}{3} \right]^a_0\]
Therefore, Area of OACO \[= \frac{2\sqrt{5} a^\frac{3}{2}}{3}\]
Similarly approximating the area of CABC the length \[=\left| y_2 \right|\] and the width = dx
\[\text{Area of CABC }= \int_a^\frac{6}{\sqrt{5}} \left| y_2 \right| d x\]
\[= \int_a^\frac{6}{\sqrt{5}} y_2 d x\]
Area of CABC\[= \frac{9\pi}{5} - \frac{a}{2}\sqrt{\frac{36}{5} - a^2} - \frac{18}{5} \sin^{- 1} \left( \frac{a\sqrt{5}}{6} \right)\]
Thus the Required area, A = 2(Area of OACO + Area of CABC)
APPEARS IN
संबंधित प्रश्न
Using integration, find the area bounded by the curve x2 = 4y and the line x = 4y − 2.
Find the area bounded by the curve y = sin x between x = 0 and x = 2π.
Find the equation of a curve passing through the point (0, 2), given that the sum of the coordinates of any point on the curve exceeds the slope of the tangent to the curve at that point by 5.
Sketch the graph of y = |x + 4|. Using integration, find the area of the region bounded by the curve y = |x + 4| and x = –6 and x = 0.
Using integration, find the area of the region bounded by the line 2y = 5x + 7, x-axis and the lines x = 2 and x = 8.
Sketch the graph y = | x − 5 |. Evaluate \[\int\limits_0^1 \left| x - 5 \right| dx\]. What does this value of the integral represent on the graph.
Sketch the graph y = | x + 1 |. Evaluate\[\int\limits_{- 4}^2 \left| x + 1 \right| dx\]. What does the value of this integral represent on the graph?
Find the area bounded by the ellipse \[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\] and the ordinates x = ae and x = 0, where b2 = a2 (1 − e2) and e < 1.
Find the area of the region bounded by x2 + 16y = 0 and its latusrectum.
Find the area of the region common to the parabolas 4y2 = 9x and 3x2 = 16y.
Find the area enclosed by the parabolas y = 5x2 and y = 2x2 + 9.
Find the area of the region bounded by \[y = \sqrt{x}\] and y = x.
Find the area bounded by the parabola y = 2 − x2 and the straight line y + x = 0.
Using the method of integration, find the area of the region bounded by the following lines:
3x − y − 3 = 0, 2x + y − 12 = 0, x − 2y − 1 = 0.
Find the area of the region bounded by the curve y = \[\sqrt{1 - x^2}\], line y = x and the positive x-axis.
Find the area of the region between the parabola x = 4y − y2 and the line x = 2y − 3.
The area bounded by the curve y = loge x and x-axis and the straight line x = e is ___________ .
The area bounded by the curve y = 4x − x2 and the x-axis is __________ .
The area bounded by the curve y = f (x), x-axis, and the ordinates x = 1 and x = b is (b −1) sin (3b + 4). Then, f (x) is __________ .
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices area A(1, 2), B (2, 0) and C (4, 3).
Find the coordinates of a point of the parabola y = x2 + 7x + 2 which is closest to the straight line y = 3x − 3.
Find the area of the curve y = sin x between 0 and π.
Find the area of the region bounded by the curves y2 = 9x, y = 3x
Find the area of the region bounded by the curve y2 = 4x, x2 = 4y.
Find the area enclosed by the curve y = –x2 and the straight lilne x + y + 2 = 0
The area of the region bounded by the curve x2 = 4y and the straight line x = 4y – 2 is ______.
Using integration, find the area of the region in the first quadrant enclosed by the line x + y = 2, the parabola y2 = x and the x-axis.
The curve x = t2 + t + 1,y = t2 – t + 1 represents
The area of the region enclosed by the parabola x2 = y, the line y = x + 2 and the x-axis, is
Area of the region bounded by the curve `y^2 = 4x`, `y`-axis and the line `y` = 3 is:
Find the area of the region enclosed by the curves y2 = x, x = `1/4`, y = 0 and x = 1, using integration.
Let T be the tangent to the ellipse E: x2 + 4y2 = 5 at the point P(1, 1). If the area of the region bounded by the tangent T, ellipse E, lines x = 1 and x = `sqrt(5)` is `sqrt(5)`α + β + γ `cos^-1(1/sqrt(5))`, then |α + β + γ| is equal to ______.
The area of the region bounded by the parabola (y – 2)2 = (x – 1), the tangent to it at the point whose ordinate is 3 and the x-axis is ______.
Sketch the region bounded by the lines 2x + y = 8, y = 2, y = 4 and the Y-axis. Hence, obtain its area using integration.
Hence find the area bounded by the curve, y = x |x| and the coordinates x = −1 and x = 1.
