Advertisements
Advertisements
प्रश्न
Sketch the graph of y = |x + 4|. Using integration, find the area of the region bounded by the curve y = |x + 4| and x = –6 and x = 0.
उत्तर
y = x + 4, if x > 4 and y = -(x+4), if x < 4
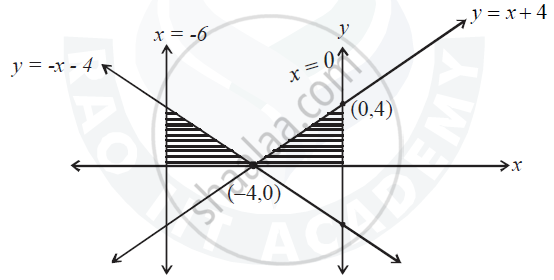
For y = x + 4
when x = 0, y= 4
and when y = 0, x = -4
Point are
∴ (0,4) and (-4,0)
For y = -x - 4
when x = 0, y = -4
when y = 0, x= -4
∴ Point are
(0, -4) and (-4,0)
∴ Required area
`= int_(-6)^(-4)-(x+4) dx + int_(-4)^0 (x + 4) dx`
`= -[x^2/2 + 4x]_(-6)^(-4) + [x^2/2 + 4x]_(-4)^0`
`= [(-4)^2/4 + 4(-4) - [(-6)^2/2 + 4(-6)]] + [0 + 0[(-4)^2/2 + 4(-4)]]`
`= -[16/2 - 16 -[36/2 - 24]] + [-(16/2 - 16)]`
= -[-8 + 6] + [8]
2 + 8 = 10 sq. unit
APPEARS IN
संबंधित प्रश्न
Find the area of the region bounded by the parabola y2 = 4ax and its latus rectum.
Using the method of integration find the area of the region bounded by lines: 2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0
The area bounded by the curve y = x | x|, x-axis and the ordinates x = –1 and x = 1 is given by ______.
[Hint: y = x2 if x > 0 and y = –x2 if x < 0]
Find the area lying above the x-axis and under the parabola y = 4x − x2.
Find the area of the region bounded by the curve xy − 3x − 2y − 10 = 0, x-axis and the lines x = 3, x = 4.
Find the area enclosed by the curve x = 3cost, y = 2sin t.
Find the area of the region in the first quadrant bounded by the parabola y = 4x2 and the lines x = 0, y = 1 and y = 4.
Find the area of the region common to the parabolas 4y2 = 9x and 3x2 = 16y.
Find the area of the region between the circles x2 + y2 = 4 and (x − 2)2 + y2 = 4.
Find the area of the region bounded by y = | x − 1 | and y = 1.
Find the area of the region enclosed between the two curves x2 + y2 = 9 and (x − 3)2 + y2 = 9.
In what ratio does the x-axis divide the area of the region bounded by the parabolas y = 4x − x2 and y = x2− x?
Find the area of the figure bounded by the curves y = | x − 1 | and y = 3 −| x |.
The area included between the parabolas y2 = 4x and x2 = 4y is (in square units)
The area bounded by the y-axis, y = cos x and y = sin x when 0 ≤ x ≤ \[\frac{\pi}{2}\] is _________ .
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using vertical strips.
The area enclosed by the circle x2 + y2 = 2 is equal to ______.
Find the area of the region bounded by the parabola y2 = 2px, x2 = 2py
Find the area of the region bounded by the curve y = x3 and y = x + 6 and x = 0
The area of the region bounded by the curve y = sinx between the ordinates x = 0, x = `pi/2` and the x-axis is ______.
If a and c are positive real numbers and the ellipse `x^2/(4c^2) + y^2/c^2` = 1 has four distinct points in common with the circle `x^2 + y^2 = 9a^2`, then
Area of the region bounded by the curve `y^2 = 4x`, `y`-axis and the line `y` = 3 is:
Find the area of the region bounded by the curve `y^2 - x` and the line `x` = 1, `x` = 4 and the `x`-axis.
Find the area of the region bounded by `x^2 = 4y, y = 2, y = 4`, and the `y`-axis in the first quadrant.
Area (in sq.units) of the region outside `|x|/2 + |y|/3` = 1 and inside the ellipse `x^2/4 + y^2/9` = 1 is ______.
Let P(x) be a real polynomial of degree 3 which vanishes at x = –3. Let P(x) have local minima at x = 1, local maxima at x = –1 and `int_-1^1 P(x)dx` = 18, then the sum of all the coefficients of the polynomial P(x) is equal to ______.
Find the area of the minor segment of the circle x2 + y2 = 4 cut off by the line x = 1, using integration.
Using integration, find the area of the region bounded by the curve y2 = 4x and x2 = 4y.
