Advertisements
Advertisements
प्रश्न
Find the area of the region bounded by the curve y = x3 and y = x + 6 and x = 0
उत्तर
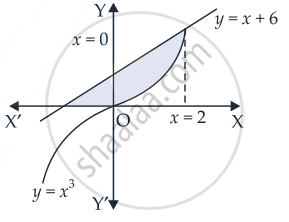
We are given that: y = x3, y = x + 6 and x = 0
Solving y = x3 and y = x + 6
We get x + 6 = x3
⇒ x3 – x – 6 = 0
⇒ x2(x – 2) + 2x(x – 2) + 3(x – 2) = 0
⇒ (x – 2)(x2 + 2x + 3) = 0
x2 + 2x + 3 = 0 has no real roots.
∴ x = 2
∴ Required area of the shaded region
= `int_0^2 (x + 6) "d"x - int_0^2 x^3 "d"x`
= `[x^2/2 + 6x]_0^2 - 1/4 [x^4]_0^2`
= `(4/2 + 12) - (0 + 0) - 1/4 [(2)^4 - 0]`
= `14 - 1/4 xx 16`
= 14 – 4
= 10 sq.units
APPEARS IN
संबंधित प्रश्न
Using the method of integration, find the area of the triangular region whose vertices are (2, -2), (4, 3) and (1, 2).
Find the area of the region bounded by the curve x2 = 16y, lines y = 2, y = 6 and Y-axis lying in the first quadrant.
Using the method of integration find the area of the region bounded by lines: 2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0
Find the area of ellipse `x^2/1 + y^2/4 = 1`
Using integration, find the area of the region bounded between the line x = 2 and the parabola y2 = 8x.
Find the area lying above the x-axis and under the parabola y = 4x − x2.
Sketch the graph y = | x + 3 |. Evaluate \[\int\limits_{- 6}^0 \left| x + 3 \right| dx\]. What does this integral represent on the graph?
Find the area of the region bounded by the curve xy − 3x − 2y − 10 = 0, x-axis and the lines x = 3, x = 4.
Find the area enclosed by the curve x = 3cost, y = 2sin t.
Find the area, lying above x-axis and included between the circle x2 + y2 = 8x and the parabola y2 = 4x.
Find the area of the region bounded by the curves y = x − 1 and (y − 1)2 = 4 (x + 1).
Find the area of the circle x2 + y2 = 16 which is exterior to the parabola y2 = 6x.
Find the area bounded by the parabola x = 8 + 2y − y2; the y-axis and the lines y = −1 and y = 3.
The area bounded by the parabola x = 4 − y2 and y-axis, in square units, is ____________ .
If An be the area bounded by the curve y = (tan x)n and the lines x = 0, y = 0 and x = π/4, then for x > 2
The area bounded by the curve y = 4x − x2 and the x-axis is __________ .
The area of the region (in square units) bounded by the curve x2 = 4y, line x = 2 and x-axis is
The area bounded by the curve y2 = 8x and x2 = 8y is ___________ .
Sketch the graphs of the curves y2 = x and y2 = 4 – 3x and find the area enclosed between them.
The area of the region bounded by the curve y = x2 and the line y = 16 ______.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2
Find the area bounded by the curve y = `sqrt(x)`, x = 2y + 3 in the first quadrant and x-axis.
Find the area bounded by the lines y = 4x + 5, y = 5 – x and 4y = x + 5.
Using integration, find the area of the region `{(x, y): 0 ≤ y ≤ sqrt(3)x, x^2 + y^2 ≤ 4}`
Find the area of the region bounded by the curve `y^2 - x` and the line `x` = 1, `x` = 4 and the `x`-axis.
Find the area of the region bounded by `y^2 = 9x, x = 2, x = 4` and the `x`-axis in the first quadrant.
The area bounded by the curve `y = x|x|`, `x`-axis and the ordinate `x` = – 1 and `x` = 1 is given by
