Advertisements
Advertisements
Question
The area of the region bounded by the circle x2 + y2 = 1 is ______.
Options
2π sq.units
π sq.units
3π sq.units
4π sq.units
Solution
The area of the region bounded by the circle x2 + y2 = 1 is π sq.units.
Explanation: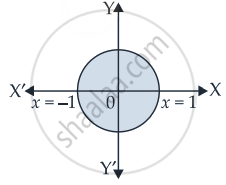
Given equation of circle is x2 + y2 = 1
⇒ y = `sqrt(1 - x^2)`
Since the circle is symmetrical about the axes.
∴ Required area = `4 xx int_0^1 sqrt(1 - x^2) "d"x`
= `4[x/2 sqrt(1 - x^2) + 1/2 sin^-1 x]_0^1`
= `4[0 + 1/2 sin^-1 (1) - 0 - 0]`
= `4 xx 1/2 xx pi/2`
= π sq.units
APPEARS IN
RELATED QUESTIONS
Find the area bounded by the curve y2 = 4ax, x-axis and the lines x = 0 and x = a.
Find the area of the region bounded by the curve y = sinx, the lines x=-π/2 , x=π/2 and X-axis
Find the area of the region bounded by the parabola y2 = 16x and the line x = 3.
Find the area of the region bounded by the curve x2 = 16y, lines y = 2, y = 6 and Y-axis lying in the first quadrant.
Find the area under the curve y = \[\sqrt{6x + 4}\] above x-axis from x = 0 to x = 2. Draw a sketch of curve also.
Sketch the region {(x, y) : 9x2 + 4y2 = 36} and find the area of the region enclosed by it, using integration.
Using integration, find the area of the region bounded by the following curves, after making a rough sketch: y = 1 + | x + 1 |, x = −2, x = 3, y = 0.
Find the area of the region bounded by x2 = 16y, y = 1, y = 4 and the y-axis in the first quadrant.
Find the area of the region bounded by the curve \[a y^2 = x^3\], the y-axis and the lines y = a and y = 2a.
Using integration, find the area of the region bounded by the triangle ABC whose vertices A, B, C are (−1, 1), (0, 5) and (3, 2) respectively.
Using integration, find the area of the triangular region, the equations of whose sides are y = 2x + 1, y = 3x+ 1 and x = 4.
Find the area of the region between the circles x2 + y2 = 4 and (x − 2)2 + y2 = 4.
Find the area of the region in the first quadrant enclosed by x-axis, the line y = \[\sqrt{3}x\] and the circle x2 + y2 = 16.
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2= 32.
Make a sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 3; 0 ≤ y ≤ 2x + 3; 0 ≤ x ≤ 3} and find its area using integration.
Using integration find the area of the region bounded by the curves \[y = \sqrt{4 - x^2}, x^2 + y^2 - 4x = 0\] and the x-axis.
The area included between the parabolas y2 = 4x and x2 = 4y is (in square units)
The area bounded by the parabola y2 = 4ax and x2 = 4ay is ___________ .
The area bounded by the curve y = x4 − 2x3 + x2 + 3 with x-axis and ordinates corresponding to the minima of y is _________ .
Find the area of the region bounded by the curve ay2 = x3, the y-axis and the lines y = a and y = 2a.
Find the area of the region bounded by the parabolas y2 = 6x and x2 = 6y.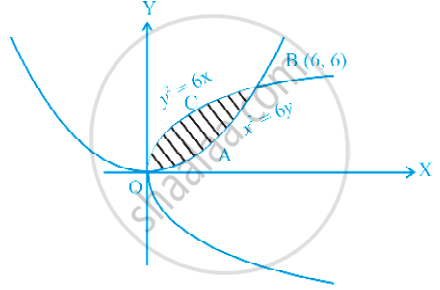
Find the area bounded by the curve y = 2cosx and the x-axis from x = 0 to x = 2π
The area of the region enclosed by the parabola x2 = y, the line y = x + 2 and the x-axis, is
Find the area of the region bounded by curve 4x2 = y and the line y = 8x + 12, using integration.
Area (in sq.units) of the region outside `|x|/2 + |y|/3` = 1 and inside the ellipse `x^2/4 + y^2/9` = 1 is ______.
Let f : [–2, 3] `rightarrow` [0, ∞) be a continuous function such that f(1 – x) = f(x) for all x ∈ [–2, 3]. If R1 is the numerical value of the area of the region bounded by y = f(x), x = –2, x = 3 and the axis of x and R2 = `int_-2^3 xf(x)dx`, then ______.
Let a and b respectively be the points of local maximum and local minimum of the function f(x) = 2x3 – 3x2 – 12x. If A is the total area of the region bounded by y = f(x), the x-axis and the lines x = a and x = b, then 4A is equal to ______.
Make a rough sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 1, 0 ≤ y ≤ x + 1, 0 ≤ x ≤ 2} and find the area of the region, using the method of integration.
Using integration, find the area bounded by the curve y2 = 4ax and the line x = a.
Using integration, find the area of the region bounded by the curve y2 = 4x and x2 = 4y.
