Question

Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x² + y²= 32.

Answer 1

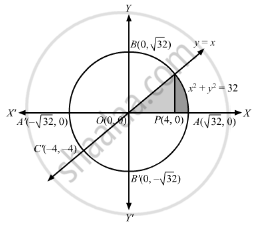
We have,
\[x^2 + y^2 = 32\] and \[y = x\]
The point of intersection of the circle and parabola is obtained by solving the two equations
\[\therefore x^2 + x^2 = 32\]
\[ \Rightarrow 2 x^2 = 32 \]
\[ \Rightarrow x^2 = 16 \]
\[ \Rightarrow x = \pm 4 \]
\[ \therefore y = \pm 4 \]
\[\text{ Thus C }\left( 4, 4 \right)\text{ and C' }\left( - 4, - 4 \right)\text{ are points of intersection of the circle and straight line .} \]
\[\text{ Required shaded area }\left( OCAPO \right) =\text{ area }\left( OCPO \right) +\text{ area }\left( PCAP \right)\]
\[ = \int_0^4 \left| y_1 \right|dx + \int_4^\sqrt{32} \left| y_2 \right|dx\]
\[ = \int_0^4 y_1 dx + \int_4^\sqrt{32} y_2 dx ...............\left\{ \because y_1 > 0 \Rightarrow \left| y_1 \right| = y_1\text{ and }y_2 > 0 \Rightarrow \left| y_2 \right| = y_2 \right\}\]
\[ = \int_0^4 x dx + \int_4^\sqrt{32} \sqrt{32 - x^2} dx \]
\[ = \left[ \frac{x^2}{2} \right]_0^4 + \left[ \frac{1}{2}x\sqrt{32 - x^2} + \frac{1}{2} \times 32 \sin^{- 1} \left( \frac{x}{\sqrt{32}} \right) \right]_4^\sqrt{32} \]
\[ = 8 + 8\pi - 8 - 4\pi\]
\[ = 4\pi\text{ sq units . }\]