Advertisements
Advertisements
Question
Find the area of the smaller region bounded by the curves `x^2/25 + y^2/16` = 1 and `x/5 + y/4` = 1, using integration.
Solution
`x^2/25 + y^2/16` = 1 and `x/5 + y/4` = 1
`\implies` y = `4/5 sqrt(25 - x^2)`
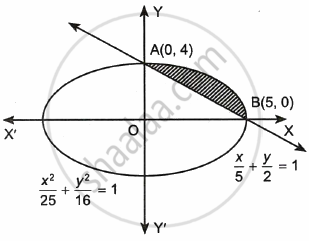
The points of intersection of the given curve and line are A(0, 4) and B(5, 0).
Area of shaded region = Area of ellipse in I quadrant – Area of triangle ΔOAB
= `int_0^5 (4/5 sqrt(25 - x^2))dx - 1/2 xx 5 xx 4`
= `4/5 [x/2 sqrt(25 - x^2) + 25/2 sin^-1 x/5]_0^5 - 10 ...[∵ int (sqrt(a^2 - x^2))dx = x/2 sqrt(a^2 - x^2) + a^2/2 sin^-1 x/a]`
= `4/5 [0 + 25/2 sin^-1 1] - 10`
= `10 xx π/2 - 10`
= (5π – 10) sq. units.
APPEARS IN
RELATED QUESTIONS
triangle bounded by the lines y = 0, y = x and x = 4 is revolved about the X-axis. Find the volume of the solid of revolution.
Prove that the curves y2 = 4x and x2 = 4y divide the area of square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.
Find the area of the region bounded by the curve x2 = 16y, lines y = 2, y = 6 and Y-axis lying in the first quadrant.
Draw a rough sketch of the graph of the curve \[\frac{x^2}{4} + \frac{y^2}{9} = 1\] and evaluate the area of the region under the curve and above the x-axis.
Find the area of the region bounded by x2 + 16y = 0 and its latusrectum.
Find the area of the region included between the parabola y2 = x and the line x + y = 2.
Prove that the area in the first quadrant enclosed by the x-axis, the line x = \[\sqrt{3}y\] and the circle x2 + y2 = 4 is π/3.
Prove that the area common to the two parabolas y = 2x2 and y = x2 + 4 is \[\frac{32}{3}\] sq. units.
Sketch the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 1. Also, find the area of this region.
Find the area of the region bounded by the curve y = \[\sqrt{1 - x^2}\], line y = x and the positive x-axis.
Find the area bounded by the lines y = 4x + 5, y = 5 − x and 4y = x + 5.
The area bounded by the curves y = sin x between the ordinates x = 0, x = π and the x-axis is _____________ .
The area of the region (in square units) bounded by the curve x2 = 4y, line x = 2 and x-axis is
Area bounded by the curve y = x3, the x-axis and the ordinates x = −2 and x = 1 is ______.
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
Area of the region bounded by the curve y2 = 4x, y-axis and the line y = 3, is
Sketch the graphs of the curves y2 = x and y2 = 4 – 3x and find the area enclosed between them.
Find the area of the region bound by the curves y = 6x – x2 and y = x2 – 2x
Using integration, find the area of the region bounded by the parabola y2 = 4x and the circle 4x2 + 4y2 = 9.
Find the area of the region bounded by the curve ay2 = x3, the y-axis and the lines y = a and y = 2a.
The area enclosed by the circle x2 + y2 = 2 is equal to ______.
Find the area of the region bounded by the curves y2 = 9x, y = 3x
Sketch the region `{(x, 0) : y = sqrt(4 - x^2)}` and x-axis. Find the area of the region using integration.
Compute the area bounded by the lines x + 2y = 2, y – x = 1 and 2x + y = 7.
Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32 is ______.
Area of the region bounded by the curve `y^2 = 4x`, `y`-axis and the line `y` = 3 is:
Sketch the region bounded by the lines 2x + y = 8, y = 2, y = 4 and the Y-axis. Hence, obtain its area using integration.
Make a rough sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 1, 0 ≤ y ≤ x + 1, 0 ≤ x ≤ 2} and find the area of the region, using the method of integration.
