Advertisements
Advertisements
Question
Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32 is ______.
Options
16π sq.units
4π sq.units
32π sq.units
24 sq.units
Solution
Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32 is 4π sq.units.
Explanation:
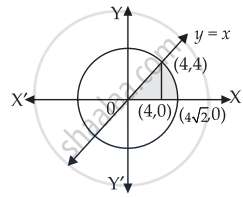
Given equation of circle is x2 + y2 = 32
⇒ x2 + y2 = `(4sqrt(2))^2` and the line is y = x and the x-axis.
Solving the two equations
We have x2 + x2 = 32
⇒ 2x2 = 32
⇒ x2 = 16
∴ x = ± 4
Required area = `int_0^4 x "d"x + int_4^(4sqrt(2)) sqrt((4sqrt(2))^2 - x^2) "d"x`
= `1/2 [x^2]_0^4 + [x/2 sqrt((4sqrt(2))^2 - x^2) + 32/2 sin^-1 x/(4sqrt(2))]_4^(4/sqrt(2))`
= `1/2 [16 - 0] + [0 + 16 sin^-1 ((4sqrt(2))/(4sqrt(2))) - 2sqrt(32 - 16) - 16sin^-1 4/(4sqrt(2))]`
= `8 + [16 sin^-1 (1) - 8 - 16sin^-1 1/sqrt(2)]`
= `8 + 16 * pi/2 - 8 - 16 * pi/4`
= `8pi - 4pi`
= 4π sq.units
APPEARS IN
RELATED QUESTIONS
Find the area of the region bounded by the parabola y2 = 4ax and its latus rectum.
Find the equation of a curve passing through the point (0, 2), given that the sum of the coordinates of any point on the curve exceeds the slope of the tangent to the curve at that point by 5
Sketch the graph of y = \[\sqrt{x + 1}\] in [0, 4] and determine the area of the region enclosed by the curve, the x-axis and the lines x = 0, x = 4.
Sketch the graph y = | x − 5 |. Evaluate \[\int\limits_0^1 \left| x - 5 \right| dx\]. What does this value of the integral represent on the graph.
Show that the areas under the curves y = sin x and y = sin 2x between x = 0 and x =\[\frac{\pi}{3}\] are in the ratio 2 : 3.
Find the area of the region in the first quadrant bounded by the parabola y = 4x2 and the lines x = 0, y = 1 and y = 4.
Prove that the area in the first quadrant enclosed by the x-axis, the line x = \[\sqrt{3}y\] and the circle x2 + y2 = 4 is π/3.
Find the area of the region bounded by \[y = \sqrt{x}\] and y = x.
Find the area of the region bounded by the curves y = x − 1 and (y − 1)2 = 4 (x + 1).
Find the area bounded by the parabola y = 2 − x2 and the straight line y + x = 0.
Using integration, find the area of the triangle ABC coordinates of whose vertices are A (4, 1), B (6, 6) and C (8, 4).
Find the area of the region bounded by the curve y = \[\sqrt{1 - x^2}\], line y = x and the positive x-axis.
If the area bounded by the parabola \[y^2 = 4ax\] and the line y = mx is \[\frac{a^2}{12}\] sq. units, then using integration, find the value of m.
The area included between the parabolas y2 = 4x and x2 = 4y is (in square units)
The area bounded by y = 2 − x2 and x + y = 0 is _________ .
The area of the region bounded by the parabola (y − 2)2 = x − 1, the tangent to it at the point with the ordinate 3 and the x-axis is _________ .
The area bounded by the parabola y2 = 4ax and x2 = 4ay is ___________ .
Using integration, find the area of the region bounded by the line x – y + 2 = 0, the curve x = \[\sqrt{y}\] and y-axis.
Find the equation of the standard ellipse, taking its axes as the coordinate axes, whose minor axis is equal to the distance between the foci and whose length of the latus rectum is 10. Also, find its eccentricity.
Find the area of the region bound by the curves y = 6x – x2 and y = x2 – 2x
Find the area of the region bounded by the curve ay2 = x3, the y-axis and the lines y = a and y = 2a.
Find the area of region bounded by the line x = 2 and the parabola y2 = 8x
Find the area of region bounded by the triangle whose vertices are (–1, 1), (0, 5) and (3, 2), using integration.
If a and c are positive real numbers and the ellipse `x^2/(4c^2) + y^2/c^2` = 1 has four distinct points in common with the circle `x^2 + y^2 = 9a^2`, then
Find the area of the region bounded by `x^2 = 4y, y = 2, y = 4`, and the `y`-axis in the first quadrant.
Find the area of the region bounded by the curve `y = x^2 + 2, y = x, x = 0` and `x = 3`
The area bounded by the curve `y = x^3`, the `x`-axis and ordinates `x` = – 2 and `x` = 1
The area of the region S = {(x, y): 3x2 ≤ 4y ≤ 6x + 24} is ______.
Make a rough sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 1, 0 ≤ y ≤ x + 1, 0 ≤ x ≤ 2} and find the area of the region, using the method of integration.
